
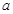 、
、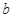 、
、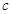 两两平行,直线
两两平行,直线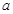 、
、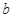 间的距离为
间的距离为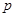 ,直线
,直线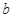 、
、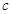 间的距离为
间的距离为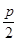 ,
,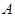 、
、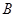 为直线
为直线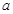 上的两个定点,且
上的两个定点,且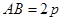 ,
,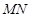 是在直线
是在直线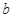 上滑动的长度为
上滑动的长度为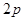 的线段.
的线段.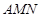 的外心
的外心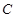 的轨迹
的轨迹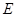 ;
;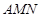 的外心
的外心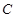 在
在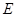 上什么位置时,使
上什么位置时,使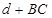 最小?最小值是多少?(其中,
最小?最小值是多少?(其中,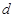 为外心
为外心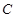 到直线
到直线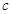 的距离)
的距离)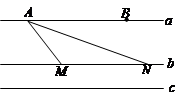
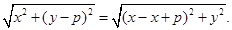
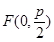 是抛物线的焦点. ∴d+|BC|=|CF|+|BC|.
是抛物线的焦点. ∴d+|BC|=|CF|+|BC|.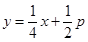 ,
,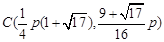 .
.  时,d+BC最小. 最小值
时,d+BC最小. 最小值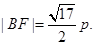


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com