
【题目】已知函数f(x)= ![]() 是定义域在R上的奇函数,且f(2)=
是定义域在R上的奇函数,且f(2)= ![]() .
.
(1)求实数a、b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)解不等式:f(log ![]() (2x﹣2)]+f[log2(1﹣
(2x﹣2)]+f[log2(1﹣ ![]() x)]≥0.
x)]≥0.
【答案】
(1)解:由题意可知f(x)定义域在R上的奇函数可得f(0)=0,f(2)= ![]()
即: 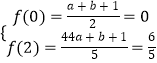 ,解得:
,解得: ![]()
即实数a=2、b=﹣3
(2)解:由(1)f(x)= ![]() =2﹣
=2﹣
函数f(x)在R上为增函数,
证明:在R上任x1,x2,且x1<x2,
则f(x1)﹣f(x2)=2﹣ ![]() ﹣(2﹣
﹣(2﹣ ![]() )=
)= ![]()
∵x1<x2,∴ ![]() ,∴
,∴ ![]() <0即f(x1)﹣f(x2)<0
<0即f(x1)﹣f(x2)<0
∴函数f(x)在R上为增函数.
(3)解:不等式:f(log ![]() (2x﹣2)]+f[log2(1﹣
(2x﹣2)]+f[log2(1﹣ ![]() x)]≥0.
x)]≥0.
等价转化为:f(log ![]() (2x﹣2)]≥﹣f[log2(1﹣
(2x﹣2)]≥﹣f[log2(1﹣ ![]() x)]
x)]
∵f(x)定义域在R上的奇函数
∴f(log ![]() (2x﹣2)]≥f[log
(2x﹣2)]≥f[log ![]() (1﹣
(1﹣ ![]() x)]
x)]
又∵函数f(x)是R上的增函数,
∴log ![]() (2x﹣2)≥log
(2x﹣2)≥log ![]() (1﹣
(1﹣ ![]() x)
x)
由 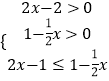
解得: ![]()
∴原不等式的解集为{x| ![]() }.
}.
【解析】1、由题意可知f(x)定义域在R上的奇函数可得f(0)=0,由已知f(2)= ![]() ,由待定系数法可求得a=2,b=3。
,由待定系数法可求得a=2,b=3。
2、根据(1)可求得函数的解析式。再根据函数增减性的定义可得证。
3、由题意转化原式可得不等式:f(log![]() (2x﹣2)]≥﹣f[log2(1﹣
(2x﹣2)]≥﹣f[log2(1﹣ ![]() x)],再根据f(x)定义域在R上的奇函数,利用奇函数的定义可得f(log
x)],再根据f(x)定义域在R上的奇函数,利用奇函数的定义可得f(log ![]() (2x﹣2)]≥f[log
(2x﹣2)]≥f[log ![]() (1﹣
(1﹣ ![]() x)],再利用函数f(x)是R上的增函数,由增函数的定义可得不等式组,解得x的取值范围。
x)],再利用函数f(x)是R上的增函数,由增函数的定义可得不等式组,解得x的取值范围。
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为y2=4x,直线L过定点P(﹣2,1),斜率为k.当k为何值时直线与抛物线:
(1)只有一个公共点;
(2)有两个公共点;
(3)没有公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
(3)为了研究喜欢打蓝球是否与性别有关,计算出K2 , 你有多大的把握认为是否喜欢打蓝球与性别有关? 附: ![]()
下面的临界值表供参考:
p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,﹣1].
(1)求m的值;
(2)若a,b,c∈R,且 ![]() +
+ ![]() +
+ ![]() =m,求证:a2+b2+c2≥36.
=m,求证:a2+b2+c2≥36.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数f(x)的单调区间和极值;
(2)若函数y=g(x)对任意x满足g(x)=f(4﹣x),求证:当x>2,f(x)>g(x);
(3)若x1≠x2 , 且f(x1)=f(x2),求证:x1+x2>4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com