
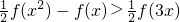 .
.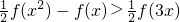 ,f
,f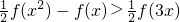 ,f(x2)-f(3x)>2f(x),由已知得:f[2(x)]=2f(x)∴f(x2-3x)>f(2x),由(2)中的单调性转化为x2-3x<2x.最后按照二次不等式两根的大小解不等式即可.
,f(x2)-f(3x)>2f(x),由已知得:f[2(x)]=2f(x)∴f(x2-3x)>f(2x),由(2)中的单调性转化为x2-3x<2x.最后按照二次不等式两根的大小解不等式即可.

 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )>
)> [f(x1)+f(x2)],则称f(x)为定义域上的凸函数.
[f(x1)+f(x2)],则称f(x)为定义域上的凸函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省大庆市铁人中学高三(上)第二次段考数学试卷(解析版) 题型:选择题
 ,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;
,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com