
| A. | 1 | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
分析 由题意,先求|$\overrightarrow{a}$|2,然后开方求模.
解答 解:因为$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是互相垂直的两个单位向量,所以$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=0,又$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,则|$\overrightarrow{a}$|2=$4{\overrightarrow{{e}_{1}}}^{2}-4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{\overrightarrow{{e}_{2}}}^{2}$=4-0+1=5;所以|$\overrightarrow{a}$|=$\sqrt{5}$;
故选:B.
点评 本题考查了平面向量模的求法;解答本题的关键是利用$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的模及数量积表示|$\overrightarrow{a}$|2.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{xsinx+cosx}{{x}^{2}}$ | B. | $\frac{xcosx+sinx}{{x}^{2}}$ | C. | $\frac{xcosx-sinx}{{x}^{2}}$ | D. | $\frac{xsinx-cosx}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 28 | 34 | 24 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
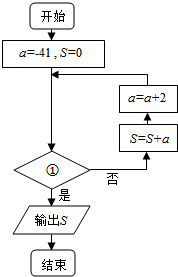
| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | C. | 增函数 | D. | 减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com