
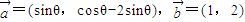 .
. ,求tanθ的值;
,求tanθ的值; ,求θ的值;
,求θ的值;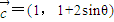 ,若
,若 ,求f(θ)的值域.
,求f(θ)的值域. .
.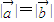 ,化简可得-sinθcosθ=cos2θ,故 cosθ=0,或 sinθ=-cosθ,由此求得θ的值.
,化简可得-sinθcosθ=cos2θ,故 cosθ=0,或 sinθ=-cosθ,由此求得θ的值.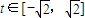 ,则 f(t)=t2+2t+2,利用二次函数的性质求出f(θ)的值域.
,则 f(t)=t2+2t+2,利用二次函数的性质求出f(θ)的值域.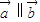 ,∴2sinθ=cosθ-2sinθ,∴
,∴2sinθ=cosθ-2sinθ,∴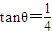 .
.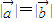 ,∴sin2θ+(cosθ-2sinθ)2=5,化简可得-sinθcosθ=cos2θ,
,∴sin2θ+(cosθ-2sinθ)2=5,化简可得-sinθcosθ=cos2θ,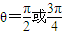 .
.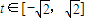 ,则有f(t)=t2+2t+2,利用二次函数的性质可得当t=-1时,f(t)有最小值1,当t=
,则有f(t)=t2+2t+2,利用二次函数的性质可得当t=-1时,f(t)有最小值1,当t=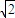 时,f(t)有最大值4+2
时,f(t)有最大值4+2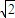 ,
,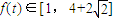 ,故f(θ)的值域为
,故f(θ)的值域为 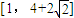 .
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2010-2011学年上海市宝山区高三第二次模拟测试理科数学卷 题型:解答题
已知向量 ,
,  ,
,  .
.
(1)若 ,求向量
,求向量 、
、 的夹角
的夹角 ;
;
(2)若 ,函数
,函数 的最大值为
的最大值为 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com