
 已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-1},x>1}\\{{x}^{2},x≤1}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-1},x>1}\\{{x}^{2},x≤1}\end{array}\right.$.科目:高中数学 来源: 题型:选择题
| A. | 57万元 | B. | 85万元 | C. | 70万元 | D. | 66万元双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,0) | C. | $(\frac{3}{2},\frac{1}{2})$ | D. | (0,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
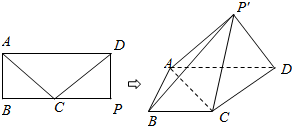 已知矩形ABPD,点C为BP的中点,AD=2,AB=1,将△CDP沿CD折起成四棱锥P′-ABCD,其中∠AP′D=90°
已知矩形ABPD,点C为BP的中点,AD=2,AB=1,将△CDP沿CD折起成四棱锥P′-ABCD,其中∠AP′D=90°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com