
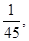 则该单位员工总数为
则该单位员工总数为 | A.110 | B.100 | C.90 | D.80 |
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:不详 题型:解答题
 加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.| 降雨量 | 70 |  110 110 | 140 | 160 | 200 | 220 |
| 频率 |  | |  | | |  |
 年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .9和0.85.若预防方案允许甲乙两种方案单独采用、联合采用或不采用,请确定预防方案使总费用最少。(总费用=采取预防措施的费用+发生突发事件损失的期望值)
.9和0.85.若预防方案允许甲乙两种方案单独采用、联合采用或不采用,请确定预防方案使总费用最少。(总费用=采取预防措施的费用+发生突发事件损失的期望值)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 自然状况 | 概率盈利方案 | A1 | A2 | A3 | A4 |
| S1 | 0.25 | 50 | 70 | -20 | 98 |
| S2 | 0.30 | 65 | 26 | 52 | 82 |
| S3 | 0.45 | 26 | 16 | 78 | -10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com