
 (必做题,每题10分)已知四棱锥
(必做题,每题10分)已知四棱锥![]() 中
中![]() 平面
平面![]() ,且
,且![]() ,底面为直角梯形,
,底面为直角梯形,![]()
![]()
![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() // 平面
// 平面![]() ;
;
(2)求截面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源:2010-2011学年江苏省姜堰市高三第一学期学情调研数学试卷 题型:解答题
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为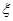 元,求
元,求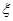 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市高三第一学期学情调研数学试卷 题型:解答题
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市高三学情调查数学试卷 题型:解答题
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
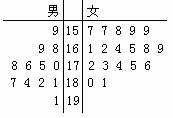
(必做题,每题10分)第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。
将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):
若身高在175cm以上(包括175cm)定义为“高个子”,
身高在175cm以下(不包括175cm)定义为“非高个子”,
且只有“女高个子”才担任“礼仪小姐”。
如果用分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
 (2)若从所有“高个子”中选3名志愿者,用
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com