
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜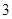 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为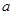 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为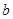 ,已知
,已知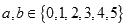 ,若
,若 ,则本次竞猜成功;
,则本次竞猜成功;
③在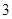 次竞猜中,至少有
次竞猜中,至少有 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从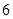 人组成的代表队中选
人组成的代表队中选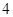 人参加此游戏,这
人参加此游戏,这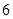 人中有且仅有
人中有且仅有 对双胞胎,记选出的
对双胞胎,记选出的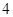 人中含有双胞胎的对数为
人中含有双胞胎的对数为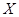 ,求
,求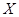 的分布列和期望.
的分布列和期望.
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11 |
| 25 |
| 11 |
| 25 |
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二第一次月考理科数学试卷 题型:选择题
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中 ,若
,若 ,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )
,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com