练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等比数列中，若a2=2，a6=162，求a10.

    思路解析一：把已知条件都用a1，q来表示，转化为关于a1，q的方程组，求出a1和q，用通项公式可以求出该等比数列中的任何一项.

    解法一：设等比数列的首项为a1，公比为q，根据题意，

    有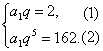

    ,得q4=81.

    ∴

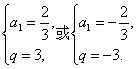
    ∴a10=a1q9=13 122.

    思路解析二：已知等比数列中的任何两项，用an=am·qn-m也可求出等比数列中的任何一项.

    解法二：∵a6=a2q4，其中a2=2，a6=162，

    ∴q4=81.

    ∴a10=a6·q4=162×81=13 122.

    思路解析三：利用结论“若三数m，n，p成等差数列，则等比数列｛an｝中的am，an，ap三项成等比（m，n，p∈N*）”求解.

    解法三：根据等比数列的性质，a2，a6，a10成等比数列，

    ∴a62=a2·a10.∴a10===162×81=13 122.

    思路解析四：利用“在等比数列中，若m+n=p+q，m，n，p，q∈N*，则aman=apaq”求解.

    解法四：∵2+10=6+6=12，∴在等比数列中，有a2·a10=a6·a6=a62，

    ∴a10==13 122.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    6、在等比数列{an}中，若a2=-2，a6=-32，则a4=
    -8
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    6、在等比数列{an}中，若a2=6，且a5-2a4-a3+12=0，则an为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等比数列{an}中，若a2=2，a6=32，则a4=
    8
    8
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等比数列{an}中，若a2•a8=36，a3+a7=15，则公比为（　　）

    查看答案和解析>>

    同步练习册答案