
在△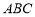 中,已知
中,已知 ,向量
,向量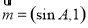 ,
,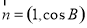 ,且
,且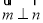 .
.
(1)求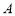 的值;
的值;
(2)若点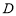 在边
在边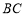 上,且
上,且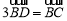 ,
,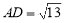 ,求△
,求△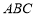 的面积.
的面积.
(1)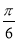 ;(2)
;(2)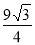 .
.
【解析】
试题分析:
解题思路:(1)先由平面向量的垂直关系得出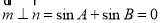 ,再利用三角形的三角关系求角A;
,再利用三角形的三角关系求角A;
(2)先由(1)中的三角关系得出三边关系,再利用余弦定理求出有关边长,进而利用三角形的面积公式求三角形的面积.
规律总结:解三角形问题,往往要综合正弦定理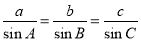 、余弦定理
、余弦定理 、三角形的面积公式
、三角形的面积公式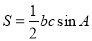 以及三角恒等变形等知识,综合性较强,主要思路是利用有关定理实现边、角的合理互化.
以及三角恒等变形等知识,综合性较强,主要思路是利用有关定理实现边、角的合理互化.
试题解析:(1)由条件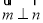 可得
可得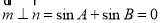 ,
,
(方法一): 由 ,A+B+C=π,所以
,A+B+C=π,所以 ,
,
又 ,所以
,所以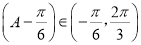 ,
,
所以 ,即
,即
(方法二):因为 ,所以
,所以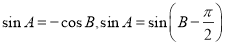
因为 ,所以
,所以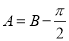 ,
,
而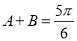 ,因此
,因此 ;
;
(2)由(1)得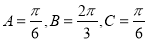 ,由正弦定理得
,由正弦定理得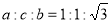 ,设
,设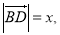 ,则
,则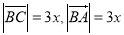 ,在
,在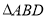 中,由余弦定理,得
中,由余弦定理,得 ,解得
,解得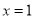 ,所以
,所以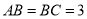 ;
;
所以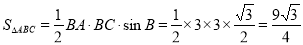 .
.
考点:1.三角形的三角关系、三边关系、边角关系2.正弦定理;3.余弦定理.


科目:高中数学 来源:2016届广东省云浮市高一5月月考文科数学试卷(解析版) 题型:选择题
已知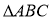 中,
中, =
= 4,
4,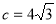 ,则
,则 ( ).
( ).
A.1500 B.300或1500 C.1200 D.600或1200
查看答案和解析>>
科目:高中数学 来源:2016届山西省忻州市高一下学期期中联考数学试卷(解析版) 题型:选择题
已知函数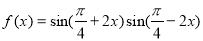 ,则函数
,则函数 的图像( )
的图像( )
A.关于点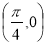 对称 B.关于点
对称 B.关于点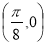 对称
对称
C.关于直线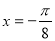 对称 D.关于直线
对称 D.关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一下学期期末考试数学试卷(解析版) 题型:选择题
△ 中,若
中,若 ,则△
,则△ 的形状为( )
的形状为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.锐角三角形
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一下学期期末考试数学试卷(解析版) 题型:选择题
已知函数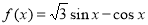 ,x∈R,若
,x∈R,若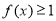 ,则x的取值范围为( ).
,则x的取值范围为( ).
A.{x|kπ+ ≤x≤kπ+π,k∈Z} B.{x|2kπ+
≤x≤kπ+π,k∈Z} B.{x|2kπ+ ≤x≤2kπ+π,k∈Z}
≤x≤2kπ+π,k∈Z}
C.{x|kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z} D.{x|2kπ+
,k∈Z} D.{x|2kπ+ ≤x≤2kπ+
≤x≤2kπ+ ,k∈Z}
,k∈Z}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com