(附加题)
(1)设集合A={1,2,3,…,10},求集合A的所有非空子集元素和的和.
(2)在区间[2,3]上,方程log2log3x=log3log2x的实根的个数共有________ 个.
解:(1)由10个元素组成的集合M={1,2,3,4,5,6,7,8,9,10},的子集有:
∅,{1},{2},{3},{4}…{1,2,3,4,5,6,7,8,9,10},…共2
10个.
先计算出包含元素1的集合:剩下的9个元素组成的集合含有2
9个子集,包括空集
而以上2
9个子集和元素1组合(含空集),又构成了集合M的所有非空子集中含元素1 的非空子集
即:在集合M的所有非空子集中,元素1出现了2
9次
同理,在集合M的所有非空子集中,元素2、3、4、5、…、10都出现了2
9次
故集合M的所有非空子集元素和的和为:
(1+2+3+4+…+10)×2
9=55×2
9=28160.
(2)令log
2log
3x=log
3log
2x=t则log
3x=2
t,log
2x=3
t,
∴
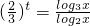
=

,∴t>0,①
又∵x∈[2,3],∴log
3x∈[log
32,1],故log
3x=2
t≤1,∴t≤0,②,
由①②可知,不存在满足条件的t,
故原方程无解.
故答案为:0.
分析:(1)由10个元素组成的集合M的子集是指属于集合的部分或所有元素组成的集合,其中包括空集.欲求集合M的所有子集的元素和的和,先计算出包含元素1的集合:剩下的9个元素组成的集合含有2
9个子集,包括空集,同理,在集合M的所有非空子集中,元素2、3、4、5、…、10都出现了2
9次,从而得出集合M的所有非空子集元素和的和.
(2)令log
2log
3x=log
3log
2x=t则log
3x=2
t,log
2x=3
t,两式相除得
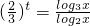
=

得出t>0;又x∈[2,3]得到t≤0,两者矛盾,从而得出原方程无解.
点评:本题主要考查子集与真子集、数列求和、根的存在性及根的个数判断等基础知识,考查运算求解能力与转化思想.属于基础题.

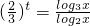 =
= ,∴t>0,①
,∴t>0,①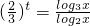 =
= 得出t>0;又x∈[2,3]得到t≤0,两者矛盾,从而得出原方程无解.
得出t>0;又x∈[2,3]得到t≤0,两者矛盾,从而得出原方程无解.
