Question

(创新题)已知函数f(x)＝，g(x)＝，

(1)证明f(x)是奇函数，并求f(x)的单调区间；

(2)分别计算f(4)－5f(2)·g(2)和f(9)－5f(3)·g(3)的值，由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明．

Answer 1

答案：
解析：

　　解：(1)证明：∵函数f(x)的定义域为(－∞，0)∪(0，＋∞)，

　　又f(－x)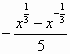＝＝＝－f(x)，

　　∴f(x)是奇函数．

　　设x₁＜x₂，且x₁，x₂∈(0，＋∞)，∴f(x₁)－f(x₂)＝

　　＝()()．

　　∵＜0，1＋＞0，

　　∴f(x₁)－f(x₂)＜0

　　∴f(x)在(0，＋∞)上单调递增．

　　又f(x)是奇函数，

　　∴f(x)在(－∞，0)上也单调递增．

　　∴f(x)的单调区间为(－∞，0)和(0，＋∞)．

　　(2)解：计算得f(4)－5f(2)·g(2)＝0，f(9)－5f(3)·g(3)＝0．

　　由此概括出对所有不等式等于零的实数x，有f(x²)－5f(x)·g(x)＝0．

　　证明如下：f(x²)－5f(x)·g(x)＝－5··

　　＝·(－)(－)＝0．