练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
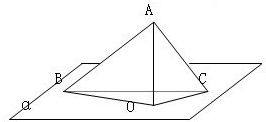
    如图所示，A∉平面α，AB、AC是平面α的两条斜线，O是A在平面α内的射影，AO=4，OC=
    		3
    ，BO⊥OC，∠OBA=30°，则C到AB的距离为
    		15
    		15
    ．
    分析：利用勾定理，根据已知，先求出△ABC的三边长，利用余弦定理求出B角的余弦，进而根据平方关系求出B的正弦，结合C到AB的距离为BC•sinB得到答案．
    解答：解：在Rt△AOB中，
    ∵AO=4，∠OBA=30°，
    ∴AB=8，OB=4
    		3

    ∵BO⊥OC，
    在Rt△BOC中，由OC=
    		3
    ，
    ∴BC=
    		51

    在Rt△AOC中，AC=
    		19

    在△ABC中，cosB=
    51+64-19
    2•
    		51
    •8
    =
    2
    		51
    17

    ∴sinB=
    		85
    17

    则C到AB的距离为BC•sinB=
    		51
    •
    		85
    17
    =
    		15

    故答案为：
    		15
    点评：本题考查的知识点是点到线的距离，其中将空间问题转化为平面解三角形问题是解答的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，在平面直角坐标系中，O为坐标原点，四边形ABCD是平行四边形，已知A（-1，-2）、B（2，3）、D（-2，-1）．
    （1）分别求两条对角线AC，BD的长度；
    （2）若向量
    AB
    -t
    OD
    与
    OD
    垂直，求实数t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，AB⊥平面BCD，∠BCD=90°则图中互相垂直的平面有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，将平面直角坐标系中的纵轴绕点O顺时针旋转300（坐标轴的长度单位不变）构成一个斜坐标系xOy，平面上任一点P关于斜坐标系的坐标（x，y）用如下方式定义：过P作两坐标轴的平行线分别交坐标轴Ox于点M，Oy于点N，则M在Ox轴上表示的数为x，N在Oy轴上表示的数为y．在斜坐标系中，若A，B两点的坐标分别为（1，2），（-2，3），则线段AB的长为
    		7
    		7
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•浦东新区一模）如图所示，在平面直角坐标系xOy上放置一个边长为1的正方形PABC，此正方形PABC沿x轴滚动（向左或向右均可），滚动开始时，点P位于原点处，设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），x∈R，该函数相邻两个零点之间的距离为m．
    （1）写出m的值并求出当0≤x≤m时，点P运动路径的长度l；
    （2）写出函数f（x），x∈[4k-2，4k+2]，k∈Z的表达式；研究该函数的性质并填写下面表格：
    函数性质 结  论
    奇偶性
    偶函数
    偶函数
    单调性 递增区间
    [4k，4k+2]，k∈z
    [4k，4k+2]，k∈z
    递减区间
    [4k-2，4k]，k∈z
    [4k-2，4k]，k∈z
    零点
    x=4k，k∈z
    x=4k，k∈z
    （3）试讨论方程f（x）=a|x|在区间[-8，8]上根的个数及相应实数a的取值范围．

    查看答案和解析>>

    同步练习册答案