
 在x=1处连续,则
在x=1处连续,则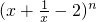 展开式中常数项是
展开式中常数项是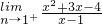 =5=n+(1)3,可得n的值,进而可得,(x+
=5=n+(1)3,可得n的值,进而可得,(x+ -2)4=(x+
-2)4=(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2),其常数项必然是4个括号中,都取(-2);或两个取x,剩下两个取(
-2),其常数项必然是4个括号中,都取(-2);或两个取x,剩下两个取( );或两个取(-2),剩下两个一个取x,一个取(
);或两个取(-2),剩下两个一个取x,一个取( );分别求出其情况数目,由加法原理计算可得答案.
);分别求出其情况数目,由加法原理计算可得答案. 在x=1处连续,
在x=1处连续,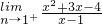 =5=n+(1)3,
=5=n+(1)3, -2)4=(x+
-2)4=(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2),
-2), );或两个取(-2),剩下两个一个取x,一个取(
);或两个取(-2),剩下两个一个取x,一个取( );
);

科目:高中数学 来源:2010年江西省南昌市新建二中高考数学二模试卷(理科)(解析版) 题型:选择题
 在x=1处连续,则
在x=1处连续,则 展开式中常数项是( )
展开式中常数项是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com