练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设变量x，y满足约束条件$\left\{{\begin{array}{l}{x+2y-5≤0}\\{x-y-2≤0}\\{x≥0}\end{array}}\right.$，则目标函数z=2x+3y的最大值是（　　）
    A．10B．9C．8D．7

    分析 确定不等式组表示的平面区域，明确目标函数的几何意义，即可求得最值．

    解答 解：约束条件对应的可行域为直线x+2y-5=0，x-y-2=0，x=0围成的三角形及其内部；

    三顶点为$（{0，\frac{5}{2}}），（{0，-2}），（{3，1}）$，
    当z=2x+3y过点（3，1）时取得最大值9，
    故选：B．

    点评 本题考查线性规划知识，考查数形结合的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=lnx-a（x-1）
    （1）若函数f（x）在（1，+∞）是单调减函数，求实数a的取值范围；
    （2）在（1）的条件下，当n∈N*时，证明：（1+$\frac{1}{2}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{3}}$）…（1+$\frac{1}{{2}^{n}}$）＜e（其中（e≈2.718…即自然对数的底数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．正方体的8个顶点两两连线所在的直线中，共构成异面直线对为174对．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．5位好朋友相约乘坐迪士尼乐园的环园小火车．小火车的车厢共有4节，设每一位乘客进入每节车厢是等可能的，则这5位好朋友无人落单（即一节车厢内，至少有5人中的2人）的概率是$\frac{31}{256}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

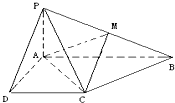    4．已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且$PA=AD=DC=\frac{1}{2}$，AB=1，M是PB的中点．
    （Ⅰ）证明：面PAD⊥面PCD；
    （Ⅱ）求三棱锥B-AMC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”．当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，那么孩子已经出生510天．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．数列{an}的前n项和a1+a2+a3+…+an可简记为$\sum_{i=1}^n{a_i}$．已知数列{an}满足a1=1，且${a_{n+1}}={a_n}+\frac{1}{n+1}$，n∈N，则$\sum_{k=1}^{2015}{k（{a_{2016}}}-{a_k}）$=1015560．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．⊙F1：（x+1）2+y2=9．⊙F2：（x-1）2+y2=1．动圆M与⊙F1内切，与⊙F2外切．
    （1）求M点的轨迹C的方程；
    （2）设动直线l：y=kx+m与曲线C交于A，B两点，（O为原点）满足|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|．对满足条件的动直线l中取两条直线l1，l2，其交点是N，当|$\overrightarrow{ON}$|=$\frac{4\sqrt{21}}{7}$时，求l1，l2的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．观察下列各式：a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…，以此类推，则当n=11时，an+bn=199．

    查看答案和解析>>

    同步练习册答案