
“抛物线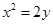 上离点
上离点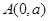 最近的点恰好为顶点”成立的充要条件是( )
最近的点恰好为顶点”成立的充要条件是( )
A.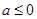 | B.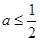 | C.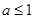 | D.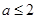 |
C
解析考点:必要条件、充分条件与充要条件的判断;抛物线的简单性质.
专题:计算题.
分析:将抛物线上的点离点A的距离用两点距离的平方表示出来,再研究二次函数的最值.
解答:解:设点P(x,y)为抛物线上的任意一点,则点P离点A(0,a)的距离的平方为
AP2=x2+(y-a)2
=x2+y2-2ay+a2
∵x2=2y
∴AP2=2y+y2-2ay+a2(y≥0)
=y2+2(1-a)y+a2(y≥0)
∴对称轴为a-1
∵离点A(0,a)最近的点恰好是顶点
∴a-1≤0解得a≤1
故选C.
点评:本题考查二次函数在给定区间的最值的求法:弄清对称轴与区间的关系,在y=0时取到最小值,故函数在定义域内递增,对称轴在区间左边.


科目:高中数学 来源: 题型:单选题
过抛物线 y2 =" 8x" 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果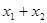 =6,那么
=6,那么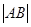 = ( *** )
= ( *** )
| A.6 | B.8 | C.9 | D.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com