练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知△ABC的三个内角A，B，C所对的边分别为a，b，c. ， ，且 ．
    （Ⅰ）求A的大小；
    （Ⅱ）若a=1， ．求S△ABC ．

    【答案】解：（Ⅰ）∵ ，∴ ，∴ ，即∴ ．
    ∵A为△ABC的内角，∴0＜A＜π，∴ ．
    （Ⅱ）若a=1， ．由余弦定理b2+c2﹣a2=2bccosA得 c2=1，
    所以
    【解析】（Ⅰ）由 ，得 ，即 ，求得 ．（Ⅱ）由a=1， ，余弦定理b2+c2﹣a2=2bccosA得 c2=1，由 求得结果．
    【考点精析】通过灵活运用数量积判断两个平面向量的垂直关系，掌握若平面的法向量为，平面的法向量为，要证，只需证，即证;即：两平面垂直两平面的法向量垂直即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，侧面ABB1A1 ， ACC1A1均为正方形，AB=AC=1，∠BAC=90，点D是棱B1C1的中点．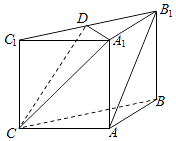
    （1）求证：AB1∥平面A1DC；
    （2）求证：A1D⊥平面BB1C1C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线： ，曲线： （为参数），以坐标原点为极点， 轴正半轴为极轴，建立极坐标系.

    （Ⅰ）求曲线， 的极坐标方程；

    （Ⅱ）曲线： （为参数， ， ）分别交， 于， 两点，当取何值时， 取得最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，与轴的正半轴交于点，右焦点， 为坐标原点，且．

    （1）求椭圆的离心率；

    （2）已知点，过点任意作直线与椭圆交于两点，设直线的斜率，若，求椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，且，设命题p：函数在上单调递减；命题q：函数 在上为增函数，

    （1）若“p且q”为真，求实数c的取值范围

    （2）若“p且q”为假，“p或q”为真，求实数c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】襄阳农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：

    襄阳农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验.

    （1）求选取的2组数据恰好是不相邻的2天数据的概率；

    （2）若选取的是12月1日与12月5日这两组数据，情根据12月2日至12月4日的数据，求关于的线性回归方程；

    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？

    注： ， .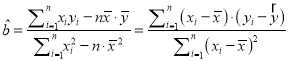

    查看答案和解析>>

    科目：高中数学 来源： 题型：

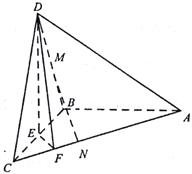
    【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC

    (1)求三棱锥D-ABC的体积

    (2)求证:平面DAC⊥平面DEF;

    (3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第年与年销量（单位：万件）之间的关系如下表：

    （1）在图中画出表中数据的散点图；

    （2）根据散点图选择合适的回归模型拟合与的关系（不必说明理由）；

    （3）建立关于的回归方程，预测第5年的销售量.

    附注：参考公式：回归直线的斜率和截距的最小二乘法估计公式分别为：

    ， .

    查看答案和解析>>

    同步练习册答案