Question

15．已知f（x）=x²-4x+3在[0，a]的值域是[-1，3]．实数a的取值范围记为集合A，g（x）=cos²x+$\frac{a}{2}$sinx．记g（x）的最大值为g（a）．若g（a）≥b，对任意实数a∈A恒成立，则实数b的取值范围是b≤$\frac{5}{4}$．

Answer 1

分析 作函数f（x）=x²-4x+3的图象，从而可得A=[2，4]；再化简g（x）=-（sinx-$\frac{a}{4}$）²+1+$\frac{{a}^{2}}{16}$，从而可得g（a）=1+$\frac{{a}^{2}}{16}$，再求g（a）的最小值即可．

解答 解：作函数f（x）=x²-4x+3的图象如下，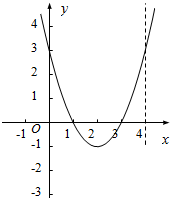
，
∵f（x）=x²-4x+3在[0，a]的值域是[-1，3]，
∴2≤a≤4，故A=[2，4]；
g（x）=cos²x+$\frac{a}{2}$sinx=1-sin²x+$\frac{a}{2}$sinx
=-（sinx-$\frac{a}{4}$）²+1+$\frac{{a}^{2}}{16}$，
∵$\frac{1}{2}$≤$\frac{a}{4}$≤1，
∴g（a）=1+$\frac{{a}^{2}}{16}$，
∵A=[2，4]，∴g_min（a）=1+$\frac{1}{4}$=$\frac{5}{4}$，
∵g（a）≥b对任意实数a∈A恒成立，
∴b≤$\frac{5}{4}$，
故答案为：b≤$\frac{5}{4}$．

点评 本题考查了二次函数的性质与应用，三角函数的最值的求法，同时考查了恒成立问题．