
在等差数列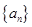 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,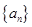 的前20项
的前20项
和S20=230.
(Ⅰ)求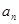 和
和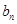 ;
;
(Ⅱ)现分别从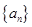 和
和 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
(Ⅰ) an=n+1 (Ⅱ) bn=2n-1
【解析】本事主要是考查了等差数列和等比数列的通项公式以及古典概型的概率的求解的综合运用。
(1)因为a1=2b1=2,b6=32, S20=230.借助于通项公式和前n项和的公式得到结论。
(2)首先分析所有的基本事件数,然后分析事件发生的基本事件数,进而结合古典概型求解概率的值。
解:(1)设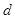 是数列
是数列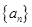 的公差,
的公差, 是
是 的公比,由题意得:
的公比,由题意得:
an=n+1, ……3分
bn=2n-1 ……7分
(2)分别从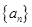 ,
, 中的前三项中各随机抽取一项,得到基本事件(2,1), (2,2), (2,4), (2,8), (3,1),
(3,2), (3,4), (3,8), (4,1), (4,2), (4,4) (4,8), (5,1), (5,2) (5,4), (5,8),有16个, ……12分
中的前三项中各随机抽取一项,得到基本事件(2,1), (2,2), (2,4), (2,8), (3,1),
(3,2), (3,4), (3,8), (4,1), (4,2), (4,4) (4,8), (5,1), (5,2) (5,4), (5,8),有16个, ……12分
符合条件的有8个,故所求概率为0.5. ……14分


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:2013-2014学年上海市高三八校联合调研考试理科数学试卷(解析版) 题型:解答题
在等差数列 和等比数列
和等比数列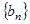 中,
中,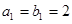 ,
, ,
, 是
是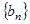 前
前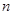 项和.
项和.
(1)若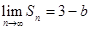 ,求实数
,求实数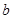 的值;
的值;
(2)是否存在正整数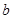 ,使得数列
,使得数列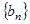 的所有项都在数列
的所有项都在数列 中?若存在,求出所有的
中?若存在,求出所有的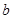 ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数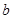 ,使得数列
,使得数列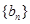 中至少有三项在数列
中至少有三项在数列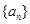 中,但
中,但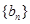 中的项不都在数列
中的项不都在数列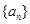 中?若存在,求出一个可能的
中?若存在,求出一个可能的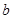 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市高三八校联合调研考试文科数学试卷(解析版) 题型:解答题
在等差数列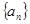 和等比数列
和等比数列 中,
中,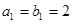 ,
,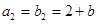 ,
, 是
是 前
前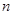 项和.
项和.
(1)若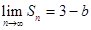 ,求实数
,求实数 的值;
的值;
(2)是否存在正整数 ,使得数列
,使得数列 的所有项都在数列
的所有项都在数列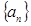 中?若存在,求出所有的
中?若存在,求出所有的 ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数 ,使得数列
,使得数列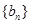 中至少有三项在数列
中至少有三项在数列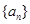 中,但
中,但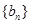 中的项不都在数列
中的项不都在数列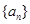 中?若存在,求出一个可能的
中?若存在,求出一个可能的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高一下学期期末考试数学试卷(解析版) 题型:解答题
在等差数列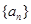 和等比数列
和等比数列 中,
中, ,
,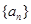 的前10项和
的前10项和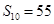 .
.
(1)求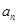 和
和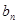 ;
;
(2)现分别从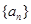 和
和 的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考(福建文))在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() 的前10项和
的前10项和![]() .
.
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)现分别从![]() 和
和![]() 的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com