
【题目】已知向量 ![]() ,记函数
,记函数 ![]() .求:
.求:
(I)函数 ![]() 的最小值及取得最小值时
的最小值及取得最小值时 ![]() 的集合;
的集合;
(II)求函数f(x) 的单调增区间。
【答案】解:由题意: ![]() ,
,
所以, ![]()
因此,
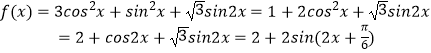
当 ![]() ,即
,即 ![]()
![]() 时,
时, ![]() 取得最小值.
取得最小值.
此时 ![]() ,
, ![]() 最小值=
最小值= ![]()
(II)函数 ![]() 的单调递增区间.
的单调递增区间.
解:由题意: ![]()
即 ![]()
于是, ![]() 的单调递增区间是
的单调递增区间是 ![]()
【解析】(1)故解集平面向量的坐标运算整理原式,再结合二倍角的余弦公式![]() 以及辅助角公式得到正弦型函数,利用正弦型函数的最值情况得出当f(x) 取得最小值和最大值时x的集合。(2)根据(1)的化简结果利用正弦型函数的单调性整体思想代入求出x的取值范围,再将其变成区间的形式。
以及辅助角公式得到正弦型函数,利用正弦型函数的最值情况得出当f(x) 取得最小值和最大值时x的集合。(2)根据(1)的化简结果利用正弦型函数的单调性整体思想代入求出x的取值范围,再将其变成区间的形式。
【考点精析】关于本题考查的二倍角的余弦公式和正弦函数的单调性,需要了解二倍角的余弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能得出正确答案.
上是减函数才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以 ![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为 ![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):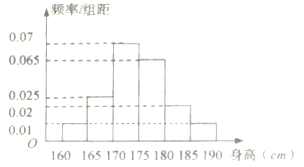
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在 ![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在 ![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线 ![]() 和直线
和直线 ![]() 交于点
交于点 ![]() .以
.以 ![]() 为起点,再从曲线
为起点,再从曲线 ![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为 ![]() .若
.若 ![]() 去九寨沟;若
去九寨沟;若 ![]() 去泰山;若
去泰山;若 ![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.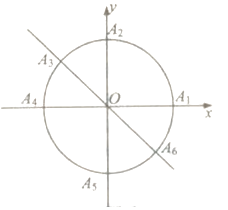
(1)若从 ![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线 ![]() 上取点
上取点 ![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点 ![]() 在曲线
在曲线 ![]() 上运动,若点
上运动,若点 ![]() 的坐标为
的坐标为 ![]() ,求
,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.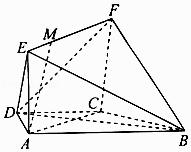
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )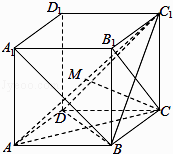
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com