
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前56项和为_____.

【答案】4084
【解析】
先利用![]() 次二项式系数对应杨辉三角形的第
次二项式系数对应杨辉三角形的第![]() 行,求出杨辉三角形的前
行,求出杨辉三角形的前![]() 项和,再结合杨辉三角形去除所有为1的项后,由最左侧一列的特征,根据等差数列求解即可.
项和,再结合杨辉三角形去除所有为1的项后,由最左侧一列的特征,根据等差数列求解即可.
![]() 次二项式系数对应杨辉三角形的第
次二项式系数对应杨辉三角形的第![]() 行,如
行,如![]() ,系数分别为1,2,1,对应杨辉三角形的第3行;
,系数分别为1,2,1,对应杨辉三角形的第3行;
令![]() ,就可以求出该行的系数之和,第一行为
,就可以求出该行的系数之和,第一行为![]() ,第二行为
,第二行为![]() ,第三行为
,第三行为![]() ,以此类推,即每一行数字和为首项为1,公比为2的等比数列;
,以此类推,即每一行数字和为首项为1,公比为2的等比数列;
则杨辉三角形的前![]() 项和为
项和为![]() ;
;
若去除所有为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成是以1为首项,以1为公差的等差数列,则![]() ;
;
由此可得,当![]() ,再加上第11行的第一项,所有项的个数为56,
,再加上第11行的第一项,所有项的个数为56,
由于最左侧为2,3,4,5,……,是以2为首项,1为公差的等差数列,故第11行的第一项为12,
又杨辉三角形的前12项的和为![]() ,
,
则此数列的前56项和为![]() .
.
故答案为4084


科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利8元.经统计,两个商家的试销情况茎叶图如下:
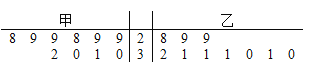
(1)现从甲商家试销的10天中抽取两天,求这两天的销售量都小于30的概率;
(2)若将频率视作概率,回答以下问题:
① 记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
② 超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①函数![]() 为奇函数;②当
为奇函数;②当![]() 时,
时,![]() ;③
;③![]() 是函数
是函数![]() 的一个零点这三个条件中任选一个,补充在下面问题中,并解答,已知函数
的一个零点这三个条件中任选一个,补充在下面问题中,并解答,已知函数![]() ,
,![]() 的图象相邻两条对称轴间的距离为
的图象相邻两条对称轴间的距离为![]() ,______.
,______.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在
在![]() 上的单调递增区间.
上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(sin(x﹣
=(sin(x﹣![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2![]()
![]() ,g(x)=f(
,g(x)=f(![]() ).
).
(1)求f(x)在[![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;

(3)结合函数的图象,写出该函数的一条性质:_________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是______.
有2个实数根,则t的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年春节期间,某服装超市举办了一次有奖促销活动,消费每超过
年春节期间,某服装超市举办了一次有奖促销活动,消费每超过![]() 元(含
元(含![]() 元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有
元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,一次性摸出
个)的抽奖盒中,一次性摸出![]() 个球,其中奖规则为:若摸到
个球,其中奖规则为:若摸到![]() 个红球,享受免单优惠;若摸出
个红球,享受免单优惠;若摸出![]() 个红球则打
个红球则打![]() 折,若摸出
折,若摸出![]() 个红球,则打
个红球,则打![]() 折;若没摸出红球,则不打折.方案二:从装有
折;若没摸出红球,则不打折.方案二:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,有放回每次摸取
个)的抽奖盒中,有放回每次摸取![]() 球,连摸
球,连摸![]() 次,每摸到
次,每摸到![]() 次红球,立减
次红球,立减![]() 元.
元.
(1)若两个顾客均分别消费了![]() 元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满![]() 元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
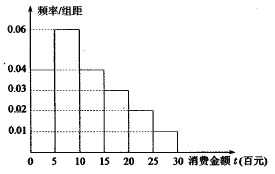
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
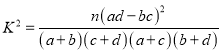 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。设![]() 表示前
表示前![]() 年的纯收入(
年的纯收入(![]() 前
前![]() 年的总收入一前
年的总收入一前![]() 年的总支出一投资额)
年的总支出一投资额)
(1)试写出![]() 的关系式.
的关系式.
(2) 该开发商从第几年开始获利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com