练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当时，有如下表达式：

    两边同时积分得：

    从而得到如下等式：

    请根据以下材料所蕴含的数学思想方法，计算：

    答案：
    解析：

    　　　由

    　　两边同时积分得：

    　　从而得到如下等式：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    (郑州一中模拟)设为奇函数，且，数列与满足如下关系：，，．

    (1)求f(x)的解析表达式；

    (2)证明：当时，有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    当时，有如下表达式:

    两边同时积分得：

    从而得到如下等式：

    请根据以下材料所蕴含的数学思想方法，计算：

    查看答案和解析>>

    科目：高中数学 来源：2013年全国普通高等学校招生统一考试理科数学（福建卷解析版） 题型：填空题

    当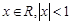时，有如下表达式：

    两边同时积分得：

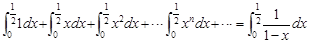
    从而得到如下等式：

    请根据以上材料所蕴含的数学思想方法，计算：

               

     

    查看答案和解析>>

    科目：高中数学 来源：2010年扬州中学高一下学期期末考试数学 题型：解答题

    （本小题满分16分） 一个三角形数表按如下方式构成：第一行依次写上n(n≥4)个数，在上一行的每相邻两数的中间正下方写上这两数之和，得到下一行，依此类推．记数表中第i行的第j个数为f(i,j)．

    (1)若数表中第i (1≤i≤n－3)行的数依次成等差数列，求证：第i+1行的数也依次成等差数列；

    (2)已知f(1,j)=4j，求f(i,1)关于i的表达式；

    (3)在(2)的条件下，若f(i,1)=(i+1)(ai－1)，bi= ，试求一个函数g(x)，使得

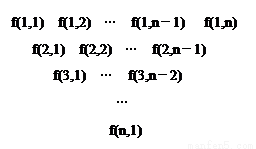    Sn=b1g(1)+b2g(2)+…+bng(n)＜，且对于任意的m∈(,)，均存在实数，使得当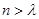时，都有Sn >m.

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案