
分析 (I)解法一:由函数图象关于直线$x=-\frac{π}{6}$对称,可得$f(-\frac{π}{3})$=f(0)=-1,进而得到a值;
解法二:利用二倍角公式和和差角(辅助角)公式,可得f(x)=asin2x-cos2x=$\sqrt{{a}^{2}+1}$sin(2x-φ),进而根据正弦函数的对称性,可得-$\frac{\sqrt{3}}{2}$a-$\frac{1}{2}$=$\sqrt{{a}^{2}+1}$,或-$\frac{\sqrt{3}}{2}$a-$\frac{1}{2}$=-$\sqrt{{a}^{2}+1}$,解得a值,可得$f(-\frac{π}{3})$的值;
(Ⅱ)当x∈$[\frac{π}{4},\frac{π}{2}]$时,2x-$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],结合正弦函数的图象和性质,可得函数f(x)在$[\frac{π}{4},\frac{π}{2}]$上的最大值和最小值.
解答 解:(Ⅰ)解法一:∵函数图象关于直线$x=-\frac{π}{6}$对称,
∴$f(-\frac{π}{3})$=f(0)=-cos20=-1,
即$\frac{1}{2}$(-$\sqrt{3}a$-$\frac{1}{2}$)+$\frac{3}{4}$=-1,
解得:a=$\sqrt{3}$,
故f(x)=cosx(2$\sqrt{3}$sinx-cosx)+sin2x
=2$\sqrt{3}$sinxcosx-cos2x+sin2x
=$\sqrt{3}$sin2x-cos2x
=2sin(2x-$\frac{π}{6}$)
解法二:∵f(x)=cosx(2asinx-cosx)+sin2x=2asinxcosx-cos2x+sin2x=asin2x-cos2x=$\sqrt{{a}^{2}+1}$sin(2x-φ)的图象的一条对称轴是直线$x=-\frac{π}{6}$.
故当$x=-\frac{π}{6}$时,asin2x-cos2x=$\sqrt{{a}^{2}+1}$,或asin2x-cos2x=-$\sqrt{{a}^{2}+1}$,
即-$\frac{\sqrt{3}}{2}$a-$\frac{1}{2}$=$\sqrt{{a}^{2}+1}$,或-$\frac{\sqrt{3}}{2}$a-$\frac{1}{2}$=-$\sqrt{{a}^{2}+1}$,
解得:a=$\sqrt{3}$,
故f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
故$f(-\frac{π}{3})$=2sin(-$\frac{5π}{6}$)=-1,
(Ⅱ)当x∈$[\frac{π}{4},\frac{π}{2}]$时,2x-$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],
故当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,函数f(x)取最大值2;
当2x-$\frac{π}{6}$=$\frac{5π}{6}$,即x=$\frac{π}{2}$时,函数f(x)取最小值1;
点评 本题考查的知识点是正弦型函数的图象和性质,二倍角公式和和差角(辅助角)公式,难度中档.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
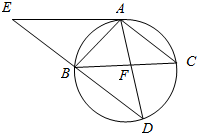 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com