
 ),函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,对定义域内任意的x,y,满足f(
),函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,对定义域内任意的x,y,满足f( )=f(x)sinα+(1-sinα)f(y),求:
)=f(x)sinα+(1-sinα)f(y),求: )及sinα的值;
)及sinα的值; ,求f(an),并猜测x∈[0,1]时,f(x)的表达式(不需证明).
,求f(an),并猜测x∈[0,1]时,f(x)的表达式(不需证明). )=f(1)sinα+(1-sinα)f(0)=sinα,
)=f(1)sinα+(1-sinα)f(0)=sinα, )=f(0)sinα+(1-sinα)f(1)=1-sinα,
)=f(0)sinα+(1-sinα)f(1)=1-sinα,
 )=1-
)=1- =
=
 ,又α∈(0,
,又α∈(0, )
)
 ),
),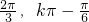 ](k∈Z).
](k∈Z). ,f(an)=f(
,f(an)=f( )(n∈N,n≥2)
)(n∈N,n≥2) ,公比为
,公比为 的等比数列,故f(an)=f(a1)•qn-1′=
的等比数列,故f(an)=f(a1)•qn-1′= ,猜测:f(x)=x.
,猜测:f(x)=x. )的值;
)的值; 看成整体进行求解即可;
看成整体进行求解即可; ,公比为
,公比为 的等比数列,即可猜测:f(x)=x.
的等比数列,即可猜测:f(x)=x.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com