
如图,![]() 、
、![]() 是相互垂直的异面直线,MN是它们的公垂线段. 点A、B在
是相互垂直的异面直线,MN是它们的公垂线段. 点A、B在![]() 上,C在
上,C在![]() 上,AM = MB = MN.
上,AM = MB = MN.
(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() ,求NB与平面ABC所成角的余弦值.
,求NB与平面ABC所成角的余弦值.
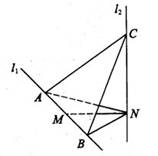
解法一:
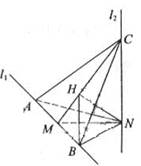 (Ⅰ)由已知l2⊥MN,l2⊥l1,MN
(Ⅰ)由已知l2⊥MN,l2⊥l1,MN![]() l1 = M,
l1 = M,
可得l2⊥平面ABN.
由已知MN⊥l1,AM = MB = MN,
可知AN = NB 且AN⊥NB又AN为
AC在平面ABN内的射影,
∴ AC⊥NB
(Ⅱ)∵ Rt △CAN = Rt △CNB,
∴ AC = BC,又已知∠ACB = 60°,
因此△ABC为正三角形。
∵ Rt △ANB = Rt △CNB。
∴ NC = NA = NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角。
在Rt △NHB中,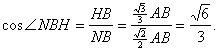
解法二:
如图,建立空间直角坐标系M-xyz,
 令 MN = 1,
令 MN = 1,
则有A(-1,0,0),B(1,0,0),N(0,1,0)。
(Ⅰ)∵MN是l1、l2的公垂线,l2⊥l1,
∴l2⊥ 平面ABN,
∴l2平行于z轴,
故可设C(0,1,m)
于是![]()
![]()
∴AC⊥NB.
(Ⅱ)![]()
又已知∠ABC = 60°,∴△ABC为正三角形,AC = BC = AB = 2.
在Rt △CNB中,NB =![]() ,可得NC =
,可得NC =![]() ,故C
,故C![]()
连结MC,作NH⊥MC于H,设H(0,λ,![]() )(λ> 0).
)(λ> 0).
![]()
![]()
![]()
![]()
∴HN ⊥平面ABC,∠NBH为NB与平面ABC所成的角.
又![]()



科目:高中数学 来源: 题型:
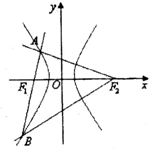 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•闸北区二模)某粮仓是如图所示的多面体,多面体的棱称为粮仓的“梁”.现测得底面ABCD是矩形,AB=16米,AD=4米,腰梁AE、BF、CF、DE分别与相交的底梁所成角均为60°.
(2013•闸北区二模)某粮仓是如图所示的多面体,多面体的棱称为粮仓的“梁”.现测得底面ABCD是矩形,AB=16米,AD=4米,腰梁AE、BF、CF、DE分别与相交的底梁所成角均为60°.查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三上学期期末考试数学理卷 题型:填空题
下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线.
 ②圆x2+y2+4x+2y+1=0与直线y=
②圆x2+y2+4x+2y+1=0与直线y=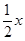 相交,所得弦长为2.
相交,所得弦长为2.
③若sin(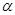 +
+ )=
)=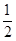 ,sin(
,sin(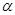 -
- )=
)= ,则tan
,则tan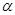 cot
cot =5.
=5.
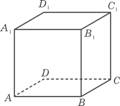
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,
P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com