
分析 (Ⅰ)对$|\overrightarrow{m}+\overrightarrow{n}|=|\overrightarrow{m}-\overrightarrow{n}|$的两边平方即可得到$\overrightarrow{m}•\overrightarrow{n}=0$,进而得出2bcosC+c-2a=0,由余弦定理便可得到$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{a}+c-2a=0$,再应用余弦定理即可求出$∠B=\frac{π}{3}$;
(Ⅱ)b=2带入a2+c2-b2-ac=0便可得出4=a2+c2-ac,根据不等式即可求出ac的范围,这样即可求出△ABC面积的范围,即得出其最大值.
解答 解:(Ⅰ)∵$|\overrightarrow{m}+\overrightarrow{n}|=|\overrightarrow{m}-\overrightarrow{n}|$;
∴$(\overrightarrow{m}+\overrightarrow{n})^{2}=(\overrightarrow{m}-\overrightarrow{n})^{2}$;
∴$\overrightarrow{m}•\overrightarrow{n}=2bcosC+c-2a=0$;
∵$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$;
∴$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{a}+c-2a=0$;
整理得,a2+c2-b2-ac=0;
∴2accosB=ac;
∴$cosB=\frac{1}{2}$;
∴$∠B=\frac{π}{3}$;
(Ⅱ)根据上面,b=2时:
4=a2+c2-ac≥2ac-ac=ac;
∴ac≤4;
∴${S}_{△ABC}=\frac{1}{2}acsin\frac{π}{3}=\frac{1}{4}ac≤1$;
即△ABC面积的最大值为1.
点评 考查向量数量积的运算,向量数量积的坐标运算,以及余弦定理,已知三角函数值求角,不等式a2+c2≥2ac的运用,以及三角形的面积公式.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).
设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年龄(岁) | 35岁及以下 | (35,50) | 50岁以上 |
| 人数(人) | 220 | 180 | 100 |
| A. | 22 | B. | 18 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
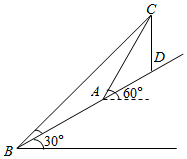 如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.
如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为40m,斜坡与水平面成30°角,则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 47,45,56 | B. | 46,45,53 | C. | 45,47,53 | D. | 46,45,56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | $\sqrt{3}$+i | D. | $\sqrt{3}$-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com