过点P(0,4)作圆x2+y2=4的切线L,L与抛物线y2=2px(p>0)交于两点A、B,且以AB为直径的圆过原点O,求P的值.
【答案】
分析:本题考查的知识点是圆的切线方程,及直线与抛物线的关系,由L过点P(0,4)与圆x
2+y
2=4的相切,则我们可以设出直线的点斜式方程,根据圆心到直线的距离等于半径,即可求出斜率的值,代入抛物线方程,即可得到交点,由于以AB为直径的圆过原点O,故
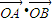
=x
1•x
2+y
1•y
2=0,代入即可求出P值.
解答:解:由已知得切线的斜率一定存在,设切线的方程为y=kx+4,即kx-y+4=0,
由于L与圆x
2+y
2=4相切,
∴圆心到直线L的距离d=
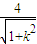
=2,解得k=
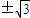
当k=

时,L的方程为:y=
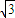
x+4
联立抛物线y
2=2px(p>0)方程后,易得:
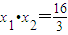
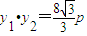
由于以AB为直径的圆过原点O
所以x
1•x
2+y
1•y
2=0
解得:P=
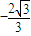
(舍去)
当k=-
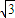
时,L的方程为:y=-
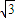
x+4
联立抛物线y
2=2px(p>0)方程后,易得:
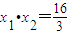
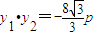
由于以AB为直径的圆过原点O
所以x
1•x
2+y
1•y
2=0
解得:P=
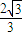
综上满足条件的P为
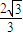 点评:
点评:解答本题要注意两个关键点:一是求过一定点的圆的切线方程,首先必须判断这点是否在圆上.若在圆上,则该点为切点,若点P(x
,y
)在圆(x-a)
2+(y-b)
2=r
2(r>0)上,则 过点P的切线方程为(x-a)(x
-a)+(y-b)(y
-b)=r
2(r>0);若在圆外,切线应有两条.一般用“圆心到切线的距离等于半径长”来解较为简单.若求出的斜率只有一个,应找出过这一点与x轴垂直的另一条切线.二是:以AB为直径的圆过原点O,故
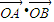
=x
1•x
2+y
1•y
2=0,

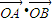 =x1•x2+y1•y2=0,代入即可求出P值.
=x1•x2+y1•y2=0,代入即可求出P值.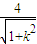 =2,解得k=
=2,解得k=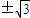
 时,L的方程为:y=
时,L的方程为:y=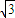 x+4
x+4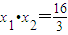
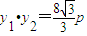
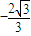 (舍去)
(舍去)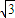 时,L的方程为:y=-
时,L的方程为:y=-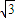 x+4
x+4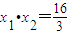
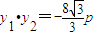
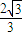
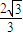
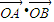 =x1•x2+y1•y2=0,
=x1•x2+y1•y2=0, 
