
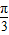 的扇形空地,现要在这块空地上种植一块矩形草皮,使其中一边在半径上且内接于扇形,问应如何设计,才能使得此草皮面积最大?并求出面积的最大值.
的扇形空地,现要在这块空地上种植一块矩形草皮,使其中一边在半径上且内接于扇形,问应如何设计,才能使得此草皮面积最大?并求出面积的最大值.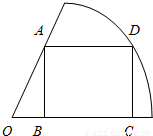
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
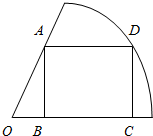 如图,在一住宅小区内,有一块半径为10米,圆心角为
如图,在一住宅小区内,有一块半径为10米,圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
某市营业区内住宅电话通话费为前3分钟0.20元,以后每分钟0.1元.(不足3分钟按3分钟计,以后不足1分钟按1分钟计)
(1)在所给坐标系中,画出一次通话在6分钟内(包括6分钟)的通话费y(元)关于通话时间t(分钟)的函数图象(如图);
(2)如果一次通话t分钟(t>0),写出通话费y(元)关于通话时间t(分钟)的函数关系式;(可用符号〈t〉表示不小于t的最小整数)
(3)如果需要通话时间较长,可以采用若干次拨打的方法.某人通话91分钟,计算这个人用最省钱的拨打方法比用一次拨打方法少花多少钱.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com