
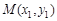 ,
,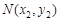 为不同的两点,直线
为不同的两点,直线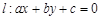 ,
,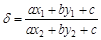 ,
, 不论
不论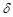 为何值,点N都不在直线
为何值,点N都不在直线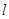 上;
上; 若
若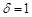 ,则过M,N的直线与直线
,则过M,N的直线与直线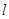 平行;
平行;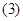 若
若 ,则直线
,则直线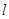 经过MN的中点;
经过MN的中点;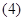 若
若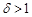 ,则点M、N在直线
,则点M、N在直线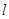 的同侧且直线
的同侧且直线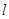 与线段MN的延长线相交.
与线段MN的延长线相交.| A.(1)(2)(3) | B.(2)(3)(4) | C.(1)(3)(4) | D.(1)(2)(3)(4) |
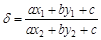 中,ax2+by2+c≠0,所以点N(x2,y2)不在直线l上,本选项正确;
中,ax2+by2+c≠0,所以点N(x2,y2)不在直线l上,本选项正确;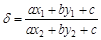 =1,化简得:y2-y1/ x2-x=-a/b,即直线MN的斜率为- a/b,
=1,化简得:y2-y1/ x2-x=-a/b,即直线MN的斜率为- a/b,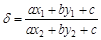 =1,
=1,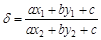 =-1,
=-1,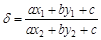 >1,
>1,

科目:高中数学 来源:不详 题型:单选题
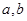 是异面直线,给出下列命题
是异面直线,给出下列命题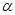 过直线
过直线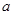 且与b平行.
且与b平行.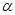 过直线
过直线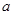 且与b垂直.
且与b垂直.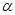 与直线
与直线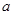 ,b都垂直.
,b都垂直.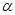 与直线
与直线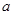 ,b的距离相等.
,b的距离相等.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
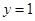 是幂函数;
是幂函数;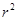 来刻画回归效果,
来刻画回归效果,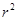 越接近0,说明模型的拟合效果越好;
越接近0,说明模型的拟合效果越好;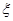 服从正态分布N(0,1),若
服从正态分布N(0,1),若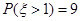 ,则
,则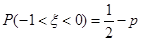 ;
;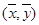
| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
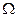 ,如果连接
,如果连接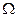 中任意两点的线段必
中任意两点的线段必 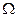 ,则称
,则称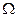 为平面上的凸集。给出平面上4个
为平面上的凸集。给出平面上4个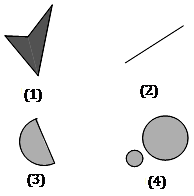
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com