
 以O为原点,
以O为原点, 所在直线为x轴,建立如图所示的直角坐标系.若
所在直线为x轴,建立如图所示的直角坐标系.若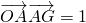 ,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).
,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).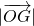 取最小值时双曲线C的方程;
取最小值时双曲线C的方程;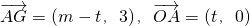 ,
,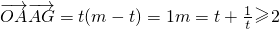 ,t∈(0,+∞)
,t∈(0,+∞)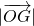 取最小值,此时G(2,3),设双曲线C的方程为
取最小值,此时G(2,3),设双曲线C的方程为 ,
, ,∴
,∴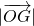 取最小值时双曲线C的方程为
取最小值时双曲线C的方程为 .
.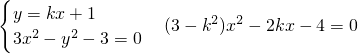 由△>0?k2<4
由△>0?k2<4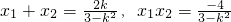 代入(*)得:
代入(*)得: ,即不存在满足条件的直线l.
,即不存在满足条件的直线l.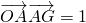 建立等式,求出m,然后根据基本不等式求出m的最小值,从而求出点G的坐标,代入双曲线方程求出b的值即可;
建立等式,求出m,然后根据基本不等式求出m的最小值,从而求出点G的坐标,代入双曲线方程求出b的值即可;

科目:高中数学 来源:高中数学综合题 题型:044
以O为原点,![]() 所在直线为x轴,建立如图所示的直角坐标系.设
所在直线为x轴,建立如图所示的直角坐标系.设![]() ,点F的坐标为
,点F的坐标为![]() ,点G的坐标为
,点G的坐标为![]() .
.

(1)求![]() 关于t的函数
关于t的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断.
的单调性,并证明你的判断.
(2)设![]() 的面积
的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取得最小值时椭圆的方程.
取得最小值时椭圆的方程.
(3)在(2)的条件下,若点P的坐标为![]() 是椭圆上的两点,且
是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
以O为原点,![]() 所在直线为
所在直线为![]() 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设![]() ,点F的坐标为
,点F的坐标为![]() ,
,![]() ,点G的坐标为
,点G的坐标为![]() 。
。
(1)求![]() 关于
关于![]() 的函数
的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断;
的单调性,并证明你的判断;
(2)设ΔOFG的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为![]() ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求x0关于t的函数x0=f(x)的表达式,判断函数f(t)的单调性,并证明你的判断;
(2)设△OFG的面积S=![]() t,若以O为中心,F为焦点的椭圆经过点G,求当|
t,若以O为中心,F为焦点的椭圆经过点G,求当|![]() |取得最小值时椭圆的方程;
|取得最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为(0,92),C、D是椭圆上的两点,且![]() =λ
=λ![]() (λ≠1),求实数λ的取值范围.
(λ≠1),求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年甘肃省白银市会宁五中高二(上)期末数学试卷(解析版) 题型:解答题
 所在直线为x轴,建立直角坐标系.设
所在直线为x轴,建立直角坐标系.设 ,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y).
,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y). ,若O以为中心,F,为焦点的椭圆经过点G,求当
,若O以为中心,F,为焦点的椭圆经过点G,求当 取最小值时椭圆的方程.
取最小值时椭圆的方程. ,C,D是椭圆上的两点,
,C,D是椭圆上的两点, ,求实数λ的取值范围.
,求实数λ的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com