Question

3．如图平面直角坐标系xOy中，椭圆$\frac{x^2}{4}+{y^2}=1$，A₁，A₂分别是椭圆的左、右两个顶点，圆A₁的半径为2，过点A₂作圆A₁的切线，切点为P，在x轴的上方交椭圆于点Q．则$\frac{PQ}{Q{A}_{2}}$=$\frac{3}{4}$．

Answer 1

分析 连结A₂P，可得△OPA₂是边长为a的正三角形，由此算出PA₁、PO的方程，联解求出点P的横坐标m=-1．由A₂P与圆A₁相切得到A₂P⊥PA₁，从而得到直线A₂P的方程，将PA₂的方程与椭圆方程联解算出Q点横坐标s=$\frac{2}{7}$．由$\frac{PQ}{Q{A}_{2}}$=$\frac{{x}_{Q}-{x}_{P}}{{x}_{{A}_{2}}-{x}_{Q}}$，把前面算出的横坐标代入即可求得$\frac{PQ}{Q{A}_{2}}$的值．

解答 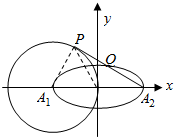解：连结PO、PA₁，可得△POA₁是边长为2的等边三角形，
∴∠PA₁O=∠POA₁=60°，可得直线PA₁的斜率k₁=tan60°=$\sqrt{3}$，
直线PO的斜率k₂=tan120°=-$\sqrt{3}$，
因此直线PA₁的方程为y=$\sqrt{3}$（x+2），直线PO的方程为y=-$\sqrt{3}$x，
设P（m，n），联解PO、PA₁的方程可得m=-1．
∵圆A₁与直线PA₂相切于P点，
∴PA₂⊥PA₁，可得∠PA₂O=90°-∠PA₁O=30°，
直线PA₂的斜率k=tan150°=-$\frac{\sqrt{3}}{3}$，因此直线PA₂的方程为y=-$\frac{\sqrt{3}}{3}$（x-2），
代入椭圆$\frac{x^2}{4}+{y^2}=1$，消去y，得$\frac{7}{3}$x²-$\frac{16}{3}$x+$\frac{4}{3}$=0，解之得x=2或x=$\frac{2}{7}$．
∵直线PA₂交椭圆于A₂（2，0）与Q点，∴设Q（s，t），可得s=$\frac{2}{7}$．
由此可得$\frac{PQ}{Q{A}_{2}}$=$\frac{{x}_{Q}-{x}_{P}}{{x}_{{A}_{2}}-{x}_{Q}}$=$\frac{s-m}{2-s}$=$\frac{\frac{2}{7}+1}{2-\frac{2}{7}}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．

点评 本题给出与椭圆相关的直线与圆相切的问题，求线段的比值．着重考查了直线的基本量与基本形式、直线与圆的位置关系、椭圆的标准方程与简单几何性质等知识，属于中档题．