
已知函数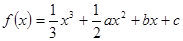 在
在 处取得极大值,在
处取得极大值,在 处取得极小值,满足
处取得极小值,满足 ,
, ,则
,则 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
D
【解析】
试题分析:解:∵函数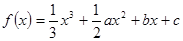 在x1处取得极大值,在x2处取得极小值,∴x1,x2是导函数f′(x)=x2+ax+b的两根,由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(-1,1),x2∈(2,4),则f′(-1)=1-a+b>0, f′(2)=4+2a+b<0, f′(4)=16+4a+b>0满足条件的约束条件的可行域如下图所示:令Z=2a+b,则ZA=3,ZB=-6,ZC=-11,故2a+b的取值范围是(-11,3)故选D
在x1处取得极大值,在x2处取得极小值,∴x1,x2是导函数f′(x)=x2+ax+b的两根,由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(-1,1),x2∈(2,4),则f′(-1)=1-a+b>0, f′(2)=4+2a+b<0, f′(4)=16+4a+b>0满足条件的约束条件的可行域如下图所示:令Z=2a+b,则ZA=3,ZB=-6,ZC=-11,故2a+b的取值范围是(-11,3)故选D
考点:导数研究函数极值
点评:本题考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力,解题时要认真审题,仔细解答


科目:高中数学 来源:2014届山东省淄博市高二下学期期中模块检测文科数学试卷(解析版) 题型:解答题
已知函数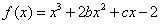 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是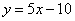 .
.
(Ⅰ)求函数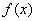 的解析式;
的解析式;
(Ⅱ)设函数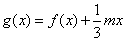 ,若
,若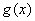 的极值存在,求实数
的极值存在,求实数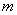 的取值范围以及当
的取值范围以及当 取何值时函数
取何值时函数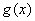 分别取得极大和极小值.
分别取得极大和极小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com