
分析 (1)由题意利用三角恒等变换化简函数的解析式,利用正弦函数的周期性求得ω可得函数的解析式,再利用正弦函数的定义域和值域求得当$x∈[{0,\frac{π}{2}}]$时,求函数f(x)的值域.
(2)由条件求得A,利用余弦定理求得bc的值,可得△ABC的面积.
解答 解:(1)∵$f(x)=\frac{{\sqrt{3}}}{2}(1+cos2ωx)+\frac{1}{2}sin2ωx=sin(2ωx+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$,∵f(x)的周期为π,且ω>0,
∴$\frac{2π}{2ω}=π$,解得ω=1,∴$f(x)=sin(2x+\frac{π}{3})+\frac{{\sqrt{3}}}{2}$.
又$0≤x≤\frac{π}{2}$,得$\frac{π}{3}≤2x+\frac{π}{3}≤\frac{4}{3}π$,$-\frac{{\sqrt{3}}}{2}≤sin(2x+\frac{π}{3})≤1$,$0≤sin(2x+\frac{π}{3})+\frac{{\sqrt{3}}}{2}≤\frac{{\sqrt{3}}}{2}+1$,
即函数f(x)在[0,$\frac{π}{2}$]上的值域为$[0,\frac{{\sqrt{3}}}{2}+1]$.
(2)∵$f(\frac{A}{2})=\sqrt{3}$,∴$sin(A+\frac{π}{3})=\frac{{\sqrt{3}}}{2}$,由A∈(0,π),知$\frac{π}{3}<A+\frac{π}{3}<\frac{4}{3}π$,
解得:$A+\frac{π}{3}=\frac{2}{3}π$,所以$A=\frac{π}{3}$.
由余弦定理知:a2=b2+c2-2bccosA,即16=b2+c2-bc,∴16=(b+c)2-3bc.
因为b+c=5,所以bc=3,∴${S_{△ABC}}=\frac{1}{2}bcsinA=\frac{3}{4}\sqrt{3}$.
点评 本题主要考查三角恒等变换,正弦函数的周期性、正弦函数的定义域和值域,余弦定理的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | g(x)=$\sqrt{x}$-1 | B. | g(x)=2x-1 | C. | $g(x)=ln({x-\frac{1}{2}})$ | D. | g(x)=4x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
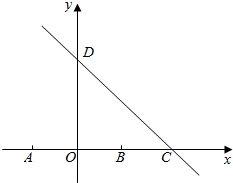 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{15}{8}$,+∞) | B. | [3,+∞) | C. | [$\frac{9}{4}$,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com