解:(I)∵

∥

,
∴2sin(A+C)(2cos
2
-1)+

cos2B=0,
又∵A+C=π-B,
∴2sinBcosB+

cos2B=0,
∴sin2B+

cos2B=0
∴tan2B=-

,
又锐角△ABC中0<B<

,0<2B<π,
∴2B=

,∴B=

;
(II)由
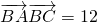
得:accosB=12,①
又由(I)知B=

,∴ac=24,②
由余弦定理得:b
2=a
2+c
2-2accosB,将b=2

及①代入得:a
2+c
2=52,
∴(a+c)
2=a
2+c
2+2ac═52+2×24=100,
∴a+c=10,③
由②③知a、c是一元二次方程t
2-10t+24=0的两个根,
解此方程,并由c>a得:a=4,c=6.
分析:(I)根据平面向量平行时满足的坐标特点,列出三角函数关系式,利用诱导公式及二倍角的正弦、余弦函数公式化简,再利用同角三角函数间的基本关系弦化切,得到tan2B的值,由三角形为锐角三角形得到B的范围,进而求出2B的范围,,利用特殊角的三角函数值即可求出B的度数;
(II)根据平面向量数量积的运算法则计算
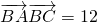
的左边得到一个等式,记作①,把B的度数代入求出ac的值,记作②,然后利用余弦定理表示出b
2,把b,ac及cosB的值代入求出a
2+c
2的值,利用完全平方公式表示出(a+c)
2,把相应的值代入,开方求出a+c的值,由②③可知a与c为一个一元二次方程的两个解,求出方程的解,根据c大于a,可得出a与c的值.
点评:此题考查了余弦定理,平面向量的数量积运算,同角三角函数间的基本关系,二倍角的正弦、余弦函数公式,以及特殊角的三角函数值,熟练掌握公式及定理是解本题的关键.同时注意完全平方公式的灵活运用.

 ),n=(cos2B,2cos2
),n=(cos2B,2cos2 -1),且向量m,n共线.
-1),且向量m,n共线.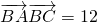 ,B=2
,B=2 ,求a,c(其中a<c)
,求a,c(其中a<c) ∥
∥ ,
, -1)+
-1)+ cos2B=0,
cos2B=0, cos2B=0,
cos2B=0, cos2B=0
cos2B=0 ,
, ,0<2B<π,
,0<2B<π, ,∴B=
,∴B= ;
;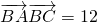 得:accosB=12,①
得:accosB=12,① ,∴ac=24,②
,∴ac=24,② 及①代入得:a2+c2=52,
及①代入得:a2+c2=52,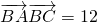 的左边得到一个等式,记作①,把B的度数代入求出ac的值,记作②,然后利用余弦定理表示出b2,把b,ac及cosB的值代入求出a2+c2的值,利用完全平方公式表示出(a+c)2,把相应的值代入,开方求出a+c的值,由②③可知a与c为一个一元二次方程的两个解,求出方程的解,根据c大于a,可得出a与c的值.
的左边得到一个等式,记作①,把B的度数代入求出ac的值,记作②,然后利用余弦定理表示出b2,把b,ac及cosB的值代入求出a2+c2的值,利用完全平方公式表示出(a+c)2,把相应的值代入,开方求出a+c的值,由②③可知a与c为一个一元二次方程的两个解,求出方程的解,根据c大于a,可得出a与c的值.
