解:(1)由已知

,所以
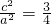
,
所以a
2=4b
2,c
2=3b
2所以
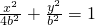
又由过焦点且垂直于长轴的直线被椭圆截得的弦长为
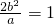
所以b=1
所以

(2)设A(x
1,y
1),B(x
2,y
2),P(x,y)
设AB:y=k(x-3)与椭圆联立得
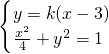
整理得(1+4k
2)x
2-24k
2x+36k
2-4=0,△=24
2k
4-16(9k
2-1)(1+4k
2)>0得
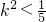

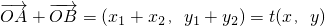

=
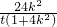
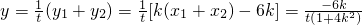
由点P在椭圆上得

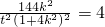
,36k
2=t
2(1+4k
2)
又由
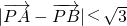
,即
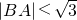
所以
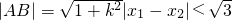
所以(1+k
2)(x
1-x
2)
2<3(1+k
2)[(x
1+x
2)
2-4x
1x
2]<3(1+k
2)

<3
整理得:(8k
2-1)(16k
2+13)>0
所以
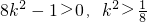
所以

由36k
2=t
2(1+4k
2)得
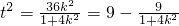
所以3<t
2<4,所以
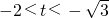
或
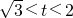
.
分析:(1)利用离心率求得a和c关系,进而利用椭圆方程中a,b和c的关系求得a和b的关系,最后利用过焦点且垂直于长轴的直线被椭圆截得的弦长求得b,则a可求得,椭圆的方程可得.
(2)设出A,B,P的坐标和AB的直线方程与椭圆的方程联立消去y,利用判别式大于0求得k的范围,利用韦达定理表示出x
1+x
2和x
1x
2,利用
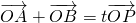
求得k和t的关系,把点P坐标代入椭圆的方程,利用
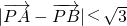
求得k的范围,进而利用k和t的关系求得t的范围.
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的过程一般是把直线与圆锥曲线的方程联立,利用韦达定理和判别式来作为解题的关键.

 的离心率为
的离心率为 ,过焦点且垂直于长轴的直线被椭圆截得的弦长为1,过点M(3,0)的直线与椭圆C相交于两点A,B,
,过焦点且垂直于长轴的直线被椭圆截得的弦长为1,过点M(3,0)的直线与椭圆C相交于两点A,B,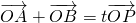 (O为坐标原点),当
(O为坐标原点),当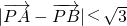 时,求实数t的取值范围.
时,求实数t的取值范围. ,所以
,所以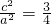 ,
,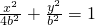
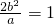

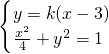
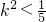

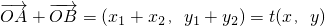
 =
=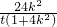
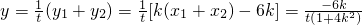

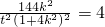 ,36k2=t2(1+4k2)
,36k2=t2(1+4k2)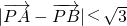 ,即
,即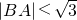
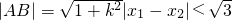
 <3
<3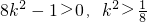

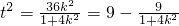
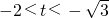 或
或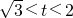 .
.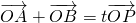 求得k和t的关系,把点P坐标代入椭圆的方程,利用
求得k和t的关系,把点P坐标代入椭圆的方程,利用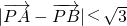 求得k的范围,进而利用k和t的关系求得t的范围.
求得k的范围,进而利用k和t的关系求得t的范围.

 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: