
 ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内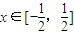 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;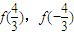 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;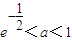 时,求方程
时,求方程 的实根.(要求说明理由
的实根.(要求说明理由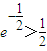 )
)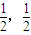 ]时,根据定义,写出f(x)的解析式;当x∈[k-
]时,根据定义,写出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,由定义知:k为与x最近的一个整数,写出解析式即可;(2)根据(1)求得
](k∈z)时,由定义知:k为与x最近的一个整数,写出解析式即可;(2)根据(1)求得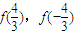 即可,利用奇偶性的定义即可判断函数f(x)(x∈R)的奇偶性,(3)要求方程
即可,利用奇偶性的定义即可判断函数f(x)(x∈R)的奇偶性,(3)要求方程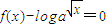 的根,即求|x-k|-
的根,即求|x-k|- logax=0的根,分类讨论,去掉绝对值符号,即可求得方程根的个数.
logax=0的根,分类讨论,去掉绝对值符号,即可求得方程根的个数.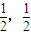 ]时,
]时, ]
] ,k+
,k+ ](k∈z)时,
](k∈z)时, ,k+
,k+ ](k∈z);
](k∈z);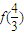 =
= ,
,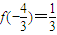
 ≤x≤k+
≤x≤k+ ,f(x)=|x-k|,
,f(x)=|x-k|, ≤x≤k+
≤x≤k+ ,可以得出-k-
,可以得出-k- ≤-x≤-k+
≤-x≤-k+ ,
, ,-k+
,-k+ ],
],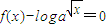 ,即|x-k|-
,即|x-k|- logax=0,
logax=0, logax,
logax, logax=0没有大于1的实根;
logax=0没有大于1的实根; logax=0的实根;
logax=0的实根;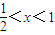 时,方程|x-k|-
时,方程|x-k|- logax=0变为1-x-
logax=0变为1-x- logax=0
logax=0 logax-(1-x)(
logax-(1-x)( )
) ,
,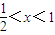 时,H(x)为减函数,H(x)>H(1)=0,
时,H(x)为减函数,H(x)>H(1)=0,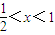 的实根;
的实根;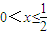 时,方程|x-k|-
时,方程|x-k|- logax=0变为x-
logax=0变为x- logax=0
logax=0 logax-x(
logax-x(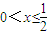 ),显然G(x)为减函数,
),显然G(x)为减函数, )=H(
)=H( )>0,
)>0,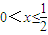 的实根.
的实根.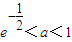 时,方程
时,方程 有且仅有一个实根,实根为1.
有且仅有一个实根,实根为1.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 1 |
| 2 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省常州市七校联考高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;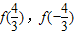 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;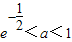 时,求方程
时,求方程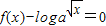 的实根.(要求说明理由
的实根.(要求说明理由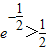 )
)查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省杭州高级中学高三第二次月考数学试卷(理科)(解析版) 题型:解答题
 ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内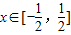 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;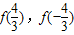 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;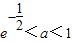 时,求方程
时,求方程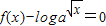 的实根.(要求说明理由
的实根.(要求说明理由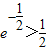 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com