
【题目】已知数列{an}是首项为1的单调递增的等比数列,且满足a3 , ![]() 成等差数列.
成等差数列.
(1)求{an}的通项公式;
(2)若bn=log3(anan+1)(n∈N*),求数列{anbn}的前n项和Sn .
【答案】
(1)解:设等比数列{an}公比为q>1,∵a3, ![]() 成等差数列.
成等差数列.
∴ ![]() a4=a3+a5,化为:3q2﹣10q+3=0,解得q=3.∴an=3n﹣1
a4=a3+a5,化为:3q2﹣10q+3=0,解得q=3.∴an=3n﹣1
(2)解:bn=log3(anan+1)= ![]() =2n﹣1,
=2n﹣1,
∴anbn=(2n﹣1)3n﹣1.
∴数列{anbn}的前n项和Sn=1+3×3+5×32+…+(2n﹣1)3n﹣1.
3Sn=3+3×32+5×33+…+(2n﹣3)3n﹣1+(2n﹣1)3n,
∴﹣2Sn=1+2(3+32+…+3n﹣1)﹣(2n﹣1)3n=1+2× ![]() ﹣(2n﹣1)3n=(2﹣2n)3n﹣2,
﹣(2n﹣1)3n=(2﹣2n)3n﹣2,
∴Sn=1+(n﹣1)3n
【解析】(1)设等比数列{an}公比为q>1,由a3 , ![]() 成等差数列.可得
成等差数列.可得 ![]() a4=a3+a5 , 化为:3q2﹣10q+3=0,解得q即可得出.(2)bn=log3(anan+1)=
a4=a3+a5 , 化为:3q2﹣10q+3=0,解得q即可得出.(2)bn=log3(anan+1)= ![]() =2n﹣1,可得anbn=(2n﹣1)3n﹣1 . 利用“错位相减法”与等比数列的求和公式即可得出.
=2n﹣1,可得anbn=(2n﹣1)3n﹣1 . 利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】通过灵活运用等比数列的通项公式(及其变式)和数列的前n项和,掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系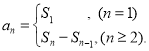 即可以解答此题.
即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,AP=AB=AC=a, ![]() ,PA⊥底面ABCD.
,PA⊥底面ABCD. 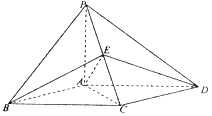
(1)求证:平面PCD⊥平面PAC;
(2)在棱PC上是否存在一点E,使得二面角B﹣AE﹣D的平面角的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值?若不存在,说明理由.
的值?若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=(x2﹣3)ex(其中x∈R,e是自然对数的底数),当t1>0时,关于x的方程[f(x)﹣t1][f(x)﹣t2]=0恰好有5个实数根,则实数t2的取值范围是( )
A.(﹣2e,0)
B.(﹣2e,0]
C.[﹣2e,6e﹣3]
D.(﹣2e,6e﹣3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题: ①若数列{an}为等差数列,Sn为其前n项和,则Sn , S2n﹣Sn , S3n﹣S2n是等差数列;
②若数列{an}为等比数列,Sn为其前n项和,则Sn , S2n﹣Sn , S3n﹣S2n是等比数列;
③若数列{an},{bn}均为等差数列,则数列{an+bn}为等差数列;
④若数列{an},{bn}均为等比数列,则数列{anbn}为等比数列
其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xoy中,点P(1,0),曲线C的参数方程为 ![]() (φ为参数).以原点O为极点,x轴的正半轴为极轴建立极坐标系,倾斜角为α的直线l的极坐标方程为ρsin(α﹣θ)=sinα.
(φ为参数).以原点O为极点,x轴的正半轴为极轴建立极坐标系,倾斜角为α的直线l的极坐标方程为ρsin(α﹣θ)=sinα.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若曲线C与直线l交于M,N两点,且 ![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开设的校本课程分别有人文科学、自然科学、艺术体育三个课程类别,每种课程类别开设课程数及学分设定如下表所示:
人文科学类 | 自然科学类 | 艺术体育类 | |
课程门数 | 4 | 4 | 2 |
每门课程学分 | 2 | 3 | 1 |
学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(Ⅰ)甲至少选1门艺术体育类课程,同时乙至多选1门自然科学类课程的概率为多少?
(Ⅱ)求甲选的3门课程正好是7学分的概率;
(Ⅲ)设甲所选3门课程的学分数为X,写出X的分布列,并求出X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() (a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1、F2 , 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时该双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=|x+2|+|x﹣1|.
(1)求f(x)的最小值及取得最小值时x的取值范围;
(2)若集合{x|f(x)+ax﹣1>0}=R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com