
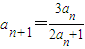 (n∈N*).
(n∈N*).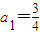 ,计算a2,a3,a4的值,并求出数列的通项公式;
,计算a2,a3,a4的值,并求出数列的通项公式;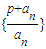 成等比数列.
成等比数列. 化简后,可求出an的值与an>0,an≠1矛盾,所以假设错误,原结论正确;
化简后,可求出an的值与an>0,an≠1矛盾,所以假设错误,原结论正确;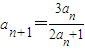 中,由a1的值即可求出a2的值,把n=2代入
中,由a1的值即可求出a2的值,把n=2代入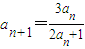 中,由a2的值即可求出a3的值,把n=4代入
中,由a2的值即可求出a3的值,把n=4代入 中,由a3的值即可求出a4的值,把已知的等式去分母后,在变形后的式子等号两边都除以3anan+1,变形后得到数列
中,由a3的值即可求出a4的值,把已知的等式去分母后,在变形后的式子等号两边都除以3anan+1,变形后得到数列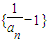 是等比数列,找出首项和公比写出此等比数列的通项公式,化简后即可得到数列的通项公式an;
是等比数列,找出首项和公比写出此等比数列的通项公式,化简后即可得到数列的通项公式an;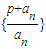 成等比数列,公比为q,根据等比数列的定义可知第n+1项与第n项的比值等于公比q,化简后根据p不为0,利用多项式为0时,各项的系数都为0即可求出p与q的值.
成等比数列,公比为q,根据等比数列的定义可知第n+1项与第n项的比值等于公比q,化简后根据p不为0,利用多项式为0时,各项的系数都为0即可求出p与q的值.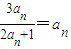 ,
, ,令n=1得:a2=
,令n=1得:a2= =
= ,
, =
=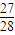 ,令n=3得:a4=
,令n=3得:a4=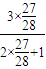 =
=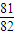 ,
,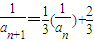 ,得
,得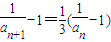 ,
,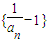 是首项为
是首项为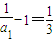 ,公比为
,公比为 的等比数列,
的等比数列,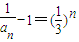 ,得
,得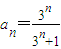 ;
;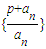 成等比数列,公比为q,
成等比数列,公比为q,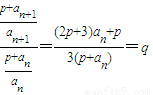 ,
,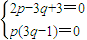 ,
,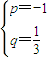 ,
,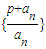 是公比为
是公比为 的等比数列.
的等比数列.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
| 3an |
| 2an+1 |
| 3 |
| 4 |
| p+an |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
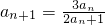 (n∈N*).
(n∈N*).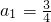 ,计算a2,a3,a4的值,并求出数列的通项公式;
,计算a2,a3,a4的值,并求出数列的通项公式;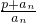 成等比数列.
成等比数列.查看答案和解析>>
科目:高中数学 来源:2011年上海市虹口区高考数学三模试卷(理科)(解析版) 题型:解答题
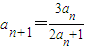 (n∈N*).
(n∈N*).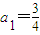 ,计算a2,a3,a4的值,并求出数列的通项公式;
,计算a2,a3,a4的值,并求出数列的通项公式;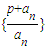 成等比数列.
成等比数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com