【答案】
分析:(1)令m=1,可得S
n-a
1=qS
n-1,S
n+1-a
1=qS
n,两式相减得:a
n+1=qa
n(n≥2),经检验对第一项也成立,从而结论成立.
(2)不妨设i,i+3,i+6,分S
i,S
i+3,S
i+6成等差数列、S
i+3,S
i,S
i+6成等差数列、S
i+3,S
i+6,S
i成等差数列这三种情况,分别求出公比q的值.
解答:解:(1)令m=1,S
n-a
1=qS
n-1,S
n+1-a
1=qS
n,两式相减得:a
n+1=qa
n(n≥2),
令n=1,a
2=qa
1,所以数列{a
n}是等比数列,
(2)不妨设公差为3的等差数列为 i,i+3,i+6,若S
i,S
i+3,S
i+6成等差数列,
则 a
i+1+a
i+2+a
i+3=a
i+4+a
i+5+a
i+6=( a
i+1+a
i+2+a
i+3 )q
3,
即 1=q
3,解得 q=1.
若S
i+3,S
i,S
i+6成等差数列,则-( a
i+1+a
i+2+a
i+3 )=( a
i+1+a
i+2+a
i+3+a
i+4+a
i+5+a
i+6 ),
∴2( a
i+1+a
i+2+a
i+3 )+( a
i+1+a
i+2+a
i+3 )q
3=0,即 2+q
3=0,解得
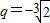
.
若S
i+3,S
i+6,S
i成等差数列,则有 ( a
i+4+a
i+5+a
i+6)=-( a
i+1+a
i+2+a
i+3+a
i+4+a
i+5+a
i+6 ),
∴2( a
i+1+a
i+2+a
i+3 )q
3+( a
i+1+a
i+2+a
i+3 )=0,∴2q
3+1=0,解得
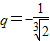
.
综上可得,q的值等于1,或等于
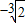
,或等于
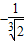
.
点评:本题主要考查等比关系的确定,等差数列的定义和性质,根据数列的递推关系求通项,体现了分类讨论的数学思想,属于中档题.

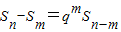 恒成立.
恒成立.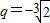 .
.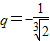 .
.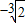 ,或等于
,或等于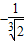 .
.

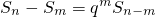 恒成立.
恒成立.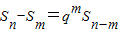 恒成立.
恒成立. 恒成立.
恒成立.