
已知点M是圆C: 上的一点,且
上的一点,且
 轴,
轴, 为垂足,点
为垂足,点 满足
满足 ,记动点
,记动点 的轨迹为曲线E.
的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若AB是曲线E的长为2的动弦,O为坐标原点,求 面积S的最大值.
面积S的最大值.
(Ⅰ)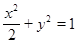 (Ⅱ)
(Ⅱ)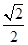
【解析】
试题分析:(Ⅰ)设N(x,y),M( ),则由已知得,
),则由已知得,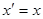 ,
,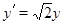 , 2分
, 2分
代入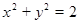 得,
得,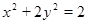 .
4分
.
4分
所以曲线E的方程为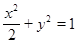 . 5分
. 5分
(Ⅱ)方法一:
因为线段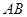 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点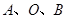 能构成三角形,
能构成三角形,
则弦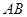 不能与
不能与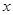 轴垂直,故可设直线
轴垂直,故可设直线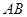 的方程为
的方程为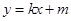 ,
,
由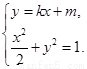 ,消去
,消去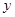 ,并整理,得
,并整理,得
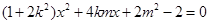 . 7分
. 7分
设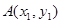 ,
,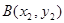 ,又
,又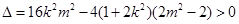 ,
,
所以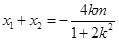 ,
,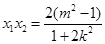 , 9分
, 9分
因为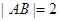 ,
,
所以 ,即
,即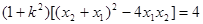 ,
,
所以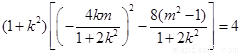 ,即
,即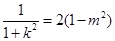 ,
,
因为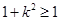 ,所以
,所以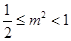 . 12分
. 12分
又点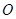 到直线
到直线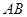 的距离
的距离 ,
,
因为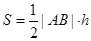
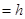 ,
,
所以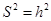
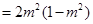
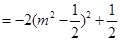 14分
14分
所以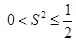 ,即
,即 的最大值为
的最大值为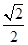 . 15分
. 15分
(Ⅱ)方法二:
因为线段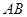 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点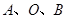 能构成三角形,
能构成三角形,
则弦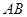 不能与
不能与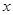 垂直,故可设直线
垂直,故可设直线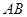 的方程为
的方程为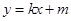 ,
,
由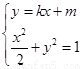 ,消去
,消去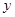 ,并整理,得
,并整理,得
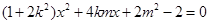 .
.
设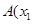 ,
, ,
,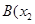 ,
,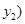 ,又
,又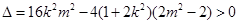 ,
,
所以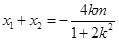 ,
,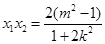 . 9分
. 9分
因为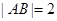 ,所以
,所以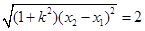 .
.
因为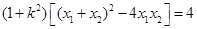 ,
,
所以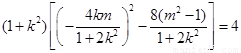 ,
,
所以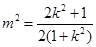 , 12分
, 12分
又点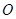 到直线
到直线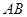 的距离
的距离 ,所以
,所以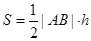
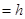 .
.
所以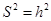
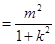
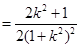
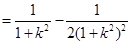 .
.
设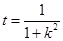 ,则
,则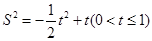 , 14分
, 14分
所以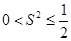 ,即
,即 的最大值为
的最大值为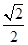 . 15分
. 15分
考点:本小题主要考查椭圆标准方程的求解,直线与椭圆的位置关系的判断和应用,弦长公式,三角形面积公式以及二次函数求最值等问题.
点评:直线与圆锥曲线的位置关系问题每年高考都会出现在压轴题的位置上,难度一般较大,关键是运算量大,所以在解决此类问题时,要注意设而不求、转化、数形结合等思想方法的综合应用.


科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点M是圆C:x2+y2=2上的一点,且MH⊥x轴,H为垂足,点N满足![]() =
=![]()
![]() ,记动点N的轨迹为曲线E.
,记动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com