
已知函数
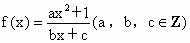 对其定义域中的任意x,都有f(-x)=-f(x)成立.又f(1)=2,f(2)<3,且f(x)在[1,+∞)上是递增的.
对其定义域中的任意x,都有f(-x)=-f(x)成立.又f(1)=2,f(2)<3,且f(x)在[1,+∞)上是递增的.
(1)
求a,b,c的值;(2)
当x<0时,讨论f(x)的单调性.|
(1) ∵f(-x)=-f(x),又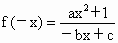 , ,
∴ 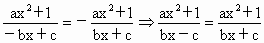 . .
比较等式两边的系数知, c=0.∴  . .
又 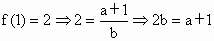 , ,
又∵ f(2)<3,f(x)在[1,+∞)上单调递增,f(1) <f(2)<3,即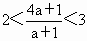 . .
将 2b=a+1,代入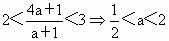 . .
又 aÎ Z,∴a=1.由2b=a+1Þ b=1.综上可知, a=b=1,c=0, . .
(2) 由(1)知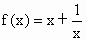 .设 .设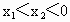 ,则 ,则
∵ 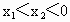 ,∴ ,∴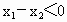 , ,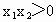 . .
要确定 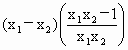 的符号,只要确定 的符号,只要确定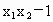 的符号即可. 的符号即可.
当 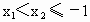 时, 时,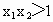 , ,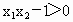 . .
此时, 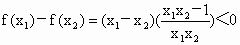 即, 即, . .
∴函数 f(x)在(-∞,-1]上是单调递增函数.当 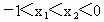 时, 时,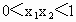 , ,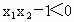 . .
此时, 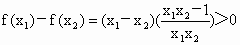 ,即 ,即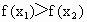 . .
∴函数 f(x)在(-1,0)上是单调递减函数.综合可知, 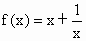 在( 在(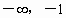 ]上递增,在(-1,0)上递减. ]上递增,在(-1,0)上递减.
讨论函数的单调性必须在其定义域内进行,即函数的单调区间是定义域的子区间,在区间内任意 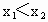 ,能判断 ,能判断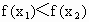 (或 (或 )才能确定其单调性. )才能确定其单调性. |


科目:高中数学 来源: 题型:
| cos2x | ||
sin(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 9 | m2-3 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
已知函数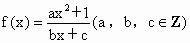 对其定义域中的任意x,都有f(-x)=-f(x)成立.又f(1)=2,f(2)<3,且f(x)在[1,+∞)上是递增的.
对其定义域中的任意x,都有f(-x)=-f(x)成立.又f(1)=2,f(2)<3,且f(x)在[1,+∞)上是递增的.
(1)求a,b,c的值;
(2)当x<0时,讨论f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省部分重点中学高三(上)起点数学试卷(理科)(钟祥一中命题)(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com