
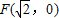 的距离与点P到定直线l:
的距离与点P到定直线l: 的距离之比为
的距离之比为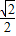 .
.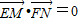 ,求|MN|的最小值.
,求|MN|的最小值.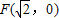 的距离与点P到定直线l:
的距离与点P到定直线l: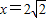 的距离之比为
的距离之比为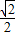 求得方程.
求得方程.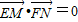 ,即6+y1y2=0.构建
,即6+y1y2=0.构建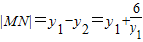 ,再利用基本不等式求得最小值.
,再利用基本不等式求得最小值.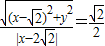 .
.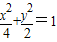 .
.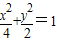 .
.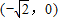 .
.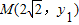 ,
,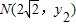 (不妨设y1>y2).
(不妨设y1>y2).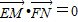 ,
,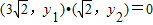 .
.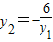 .
.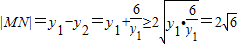 .
.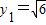 ,
, 时,等号成立.
时,等号成立.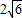 .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
4
| ||
| 3 |
| 3 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
已知动点P到直线![]() 的距离是到定点(
的距离是到定点(![]() )的距离的
)的距离的![]() 倍.
倍.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)如果直线l∶y=k(x+1)(k≠0)与P点的轨迹有两个交点A、B,求弦AB的垂直平分线在y轴上的截距y0的取值范围.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
4
| ||
| 3 |
| 3 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市树德中学高三(下)入学数学试卷(文科)(解析版) 题型:解答题
 的距离d1,是到定点F(-
的距离d1,是到定点F(- )的距离d2的
)的距离d2的 倍.
倍.查看答案和解析>>
科目:高中数学 来源:2009年北京101中学高考数学三模试卷(文科)(解析版) 题型:解答题
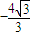 的距离d1,是到定点F(-
的距离d1,是到定点F(-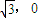 )的距离d2的
)的距离d2的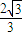 倍.
倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com