D
分析:由已知中的程序框图,分析程序的功能为:利用循环计算并输出一个数列的各项,由于此数列的通项是一个等差数列与一个等比数列的乘积构成的新数列,利用错位相减法求出数列的前n项和,进而得到答案.
解答:由已知的程序框图中,
当n=1时,输出的a=a
1=1×2
0+2×2
1;
当n=2时,输出的a=a
2=1×2
0+2×2
1+3×2
2;
当n=3时,输出的a=a
3=1×2
0+2×2
1+3×2
2+4×2
3;
…
可得数列{a
n} 的通项公式为a
n=1×2
0+2×2
1+3×2
2+4×2
3+…+(n+1)×2
n;
∵a
n=1×2
0+2×2
1+3×2
2+4×2
3+…+(n+1)×2
n,
∴2a
n=1×2
1+2×2
2+3×2
3+…+(n-2)×2
n+(n+1)×2
n+1,
∴两式相减得-a
n=2
0+2+2
2+…+2
n-(n+1)×2
n+1 ∴-a
n=

-(n+1)×2
n+1=n•2
n+1+1,
所以a
n=n•2
n+1+1,
故选D.
点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)?②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

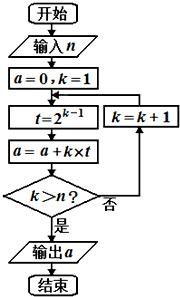 若数列{an} 的通项an由如图所示的程序框图输出的a来确定,则an=
若数列{an} 的通项an由如图所示的程序框图输出的a来确定,则an= -(n+1)×2n+1=n•2n+1+1,
-(n+1)×2n+1=n•2n+1+1,
