
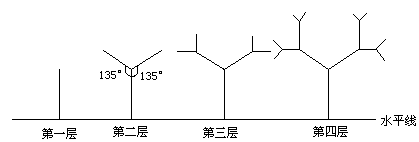
一种树形图形为:第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与线段成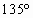 角的线段,长度为其一半;第三层按第二层的方法在第一线段的前端生成两条线段,重复前面的作法作图到第n层,设树的第n层最高点至水平线的距离为到第n层的树形的总高度.试求:
角的线段,长度为其一半;第三层按第二层的方法在第一线段的前端生成两条线段,重复前面的作法作图到第n层,设树的第n层最高点至水平线的距离为到第n层的树形的总高度.试求:
(1)到第三层及第四层的树形图的总高度;
(2)到第n层的树形图的总高度hn;
(3)若树形的高度大于2,则称树形图为“高大”,否则“矮小”,试作判断该树形是“高大”还是“矮小”呢?
 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com