
如图,在多面体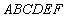 中,底面
中,底面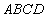 是边长为
是边长为 的的菱形,
的的菱形,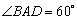 ,四边形
,四边形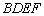 是矩形,直线BF⊥平面
是矩形,直线BF⊥平面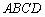 ,
,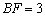 ,
,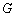 和
和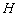 分别是
分别是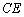 和
和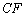 的中点.
的中点.
(Ⅰ)求证:平面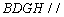 平面
平面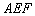 ;
;
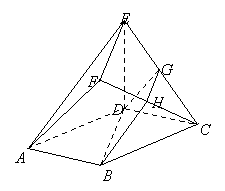 (Ⅱ)求直线CF与平面
(Ⅱ)求直线CF与平面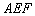 所成角的余弦值.
所成角的余弦值.
 Ⅰ)证明:在
Ⅰ)证明:在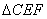 中,因为
中,因为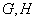 分别是
分别是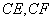 的中点,
的中点,
所以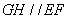 , 又因为
, 又因为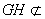 平面
平面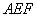 ,
,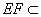 平面
平面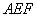 ,
,
所以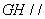 平面
平面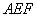 . ……………… 2分
. ……………… 2分
设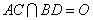 ,连接
,连接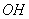 ,
,
因为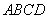 为菱形,所以
为菱形,所以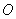 为
为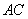 中点
中点
在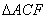 中,因为
中,因为 ,
,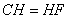 ,
,
所以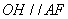 ,
,
又因为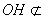 平面
平面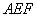 ,
,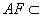 平面
平面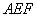 ,
,
所以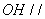 平面
平面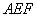 . ……………… 4分
. ……………… 4分
又因为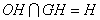 ,
,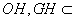 平面
平面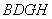 ,
,
所以平面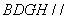 平面
平面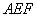 . ………………5分
. ………………5分
(Ⅱ)解:取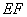 的中点
的中点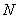 ,连接
,连接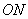 ,
,
因为四边形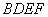 是矩形,
是矩形,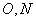 分别为
分别为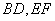 的中点,
的中点,
所以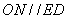 ,因为平面
,因为平面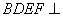 平面
平面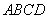 ,所以
,所以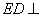 平面
平面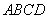 ,
,
所以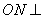 平面
平面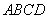 ,
,
因为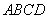 为菱形,所以
为菱形,所以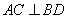 ,得
,得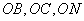 两两垂直.
两两垂直.
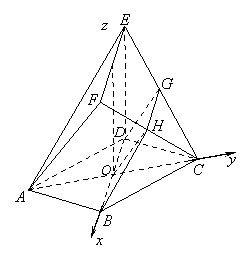
所以以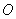 为原点,
为原点,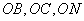 所在直线分别为
所在直线分别为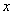 轴,
轴,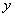 轴,
轴,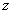 轴,
轴,
如图建立空间直角坐标系.
因为底面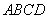 是边长为
是边长为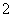 的菱形,
的菱形,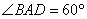 ,
,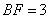 ,
,
所以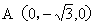 ,
,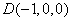 ,
,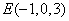 ,
,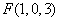 ,
,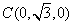 ,
,
……………………………7分
所以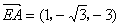 ,
, 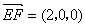 . 设平面
. 设平面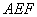 的法向量为
的法向量为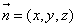 ,
,
则 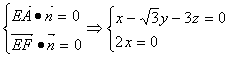
令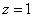 ,得
,得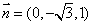 . ……………9分
. ……………9分

设直线CF与平面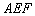 所成角为
所成角为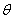
则 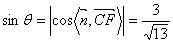 .……………11分
.……………11分
所以 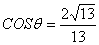 ………………12分
………………12分


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com