
(本题满分14分)定义在D上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 的上界。
的上界。
已知函数 ,
,
(1)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围;
(3)若 ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。
解:(1)当 时,
时, .
.
∵ 在
在 上递增,所以
上递增,所以 ,
,
即 在
在 上的值域为
上的值域为 . …………………………………2分
. …………………………………2分
故不存在常数 ,使
,使 成立.
成立.
所以函数 在
在 上不是有界函数. ……………………………………4分
上不是有界函数. ……………………………………4分
(2)∵函数 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数,

 在
在 上恒成立.
上恒成立.  ,
,
 在
在 上恒成立.
上恒成立.
 ……………………………6分
……………………………6分
设 ,
, ,
, .
.
由
 ,得
,得 .设
.设 ,则
,则
 ,
, ,
,
所以 在
在 上递增,
上递增, 在
在 上递减.
上递减.
 在
在 上的最大值为
上的最大值为 ,
, 在
在 上的最小值为
上的最小值为 .
.
所以实数 的取值范围为
的取值范围为 . …………………………………………… 9分
. …………………………………………… 9分
(3))方法一: ,
, .
.
∵ m>0 , ,
,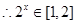 .
.
∴
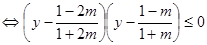 ,
,
∵
∴ .
…………………………………………11分
.
…………………………………………11分
① 当 ,即
,即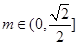 时,
时,
 ,此时
,此时 ;
;
② 当 ,即
,即 时,
时,
 ,此时
,此时 .
.
综上所述,当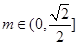 时,
时, 的取值范围是
的取值范围是 ;当
;当 时,
时, 的取值范围是
的取值范围是 ………………………………………………………14分
………………………………………………………14分
方法二:  .
.
令 ,因为
,因为 ,所以
,所以 .
.
 .
.
因为 在
在 上是减函数,所以
上是减函数,所以 .…………………11分
.…………………11分
又因为函数 在
在 上的上界是
上的上界是 ,所以
,所以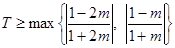 .
.
当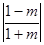

 时,
时, ,
,

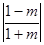
 ;
;
当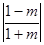

 时,
时, ,
,


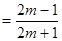 .……………………14分
.……………………14分
【解析】略


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:2011年甘肃省高一上学期期中考试数学 题型:解答题
(本题满分14分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省六校高三联考数学理卷 题型:解答题
((本题满分14分)
已知椭圆的两个焦点 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与 构成正三角形.
构成正三角形.
(1)求椭圆的方程;
(2)过点(1,0)且与坐标轴不平行的直线 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在 轴上存在定点E(
轴上存在定点E( ,0),使
,0),使 恒为定值,求
恒为定值,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学文卷 题型:解答题
(本题满分14分)
已知动圆过定点 ,且与定直线
,且与定直线 相切.
相切.
(1)求动圆圆心的轨迹 的方程;
的方程;
(2)若 是轨迹
是轨迹 的动弦,且
的动弦,且 过
过 , 分别以
, 分别以 、
、 为切点作轨迹
为切点作轨迹 的切线,设两切线交点为
的切线,设两切线交点为 ,证明:
,证明: .
.
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二第一学期期末考试文科数学 题型:解答题
(本题满分14分)
已知动圆过定点P(1,0)且与定直线 相切,点C在
相切,点C在 上.
上.
(Ⅰ)求动圆圆心M的轨迹方程;
(Ⅱ)设过点P且斜率为 的直线与曲线交于A、B两点.问直线
的直线与曲线交于A、B两点.问直线 上是否存在点C ,使得
上是否存在点C ,使得 是以
是以 为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com