分析:A.我们知道:命题“若p,则q”的逆否命题是“若¬q,则¬p”,同时注意“x=y=0”的否定是“x,y中至少有一个不为0”,据此可以判断出A的真假.
B.依据“命题:?x
0∈R,结论p成立”,则¬p为:“?x∈R,结论p的反面成立”,可以判断出B的真假.
C.由于
sinA-sinB=2cossin,因此在△ABC中,sinA>sinB?
sin>0?A>B.由此可以判断出C是否正确.
D.由向量
•=||||cos<,><0,可得
与的夹角
<,>≤π,可以判断出D是否正确.
解答:解:A.依据命题“若p,则q”的逆否命题是“若¬q,则¬p”,可知:命题“若x
2+y
2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x
2+y
2≠0”.可判断出A正确.
B.依据命题的否定法则:“命题:?x
0∈R,
-x
0+1≤0”的否定应是“?x∈R,x
2-x+1>0”,故B是真命题.
C.由于
sinA-sinB=2cossin,在△ABC中,∵0<A+B<π,∴0
<<,∴
0<cos<1,
又0<B<A<π,∴0<A-B<π,∴
0<<,∴
0<sin<1.
据以上可知:在△ABC中,sinA>sinB?
sin>0?A>B.故在△ABC中,sinA>sinB是A>B的充要条件.
因此C正确.
D.由向量
•=||||cos<,><0,∴
cos<,><0,∴
与的夹角
<,>≤π,
∴向量
与
的夹角不一定是钝角,亦可以为平角π,∴可以判断出D是错误的.
故答案是D.
点评:本题综合考查了四种命题之间的关系、命题的否定、三角形中的角大小与其相应的正弦值之间的大小关系、向量的夹角,解决问题的关键是熟练掌握其有关基础知识.



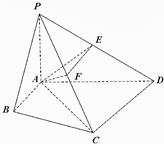 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中|?|<
(2012•包头一模)函数f(x)=sin(ωx+?)(其中|?|<