
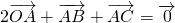 且
且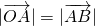 ,则向量
,则向量 在
在 方向上的投影为
方向上的投影为



 在
在 方向上的投影,根据投影的计算公式,只须求出这两个向量的夹角及向量
方向上的投影,根据投影的计算公式,只须求出这两个向量的夹角及向量 的模,借助于平面几何图形得出三角形OAB为正三角形,最后利用向量
的模,借助于平面几何图形得出三角形OAB为正三角形,最后利用向量  在
在  方向上的投影的定义即可求解.
方向上的投影的定义即可求解. 解:由题意因为△ABC的外接圆的圆心为O,半径为1,
解:由题意因为△ABC的外接圆的圆心为O,半径为1, 且
且 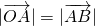 ,
, ?
? ,
, ,所以四边形ABOC为平行四边形,又由于
,所以四边形ABOC为平行四边形,又由于 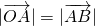 ,所以三角形OAB为正三角形且边长为1,所以四边形ABOC为边长为1且角ABO为60°的菱形,所以向量
,所以三角形OAB为正三角形且边长为1,所以四边形ABOC为边长为1且角ABO为60°的菱形,所以向量  在
在  方向上的投影为:
方向上的投影为: =
=


科目:高中数学 来源: 题型:
| 3 |
| x2 |
| 4 |
| y2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.| AB |
| AC |
| l1 |
| l2 |
| l2 |
| l1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
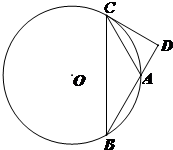 (2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
(2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=| 3 |
查看答案和解析>>
科目:高中数学 来源:2012年北京市房山区良乡中学高三数学会考模拟试卷(4)(解析版) 题型:解答题
 ,试求直线AB的方程;
,试求直线AB的方程; ,试求s的最大值.
,试求s的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com