
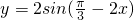 的单调递减区间是________.
的单调递减区间是________.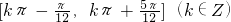
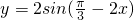 化为y=-2sin(2x-
化为y=-2sin(2x- )因此要求函数
)因此要求函数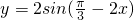 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间,故可将2x-
)的单调递增区间,故可将2x- 看成整体然后正弦函数的递增区间求不等式2kπ-
看成整体然后正弦函数的递增区间求不等式2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ 的解集即可.
的解集即可.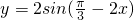
 )
)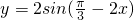 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间
)的单调递增区间 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z
,k∈z ≤x≤kπ
≤x≤kπ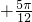 ,k∈z
,k∈z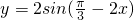 的单调递减区间是[kπ-
的单调递减区间是[kπ- ,k
,k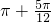 ](k∈z)
](k∈z)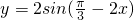 的单调递减区间.解题的关键是要注意正弦函数的自变量x的系数为正因此需利用诱导公式可将函数
的单调递减区间.解题的关键是要注意正弦函数的自变量x的系数为正因此需利用诱导公式可将函数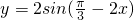 的自变量x的系数为正即y=-2sin(2x-
的自变量x的系数为正即y=-2sin(2x- ),然后要分析出函数
),然后要分析出函数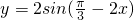 的单调递减区间即求y=2sin(2x-
的单调递减区间即求y=2sin(2x- )的单调递增区间,最后一定不要忘记k∈z!
)的单调递增区间,最后一定不要忘记k∈z! 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com